Introduzione semplificata alla Zero Knowledge

Questo libro è stato tradotto e adattato da Silvio Meneguzzo

Introduzione

Le Zero Knowledge Proofs (ZKPs, dimostrazioni a conoscenza zero) sono pura magia. Ci permettono di realizzare cose che prima non avremmo nemmeno immaginato.

Cominciamo con alcune citazioni per stuzzicare la curiosità. Alcune vi saranno familiari, altre forse no.

Ogni tecnologia sufficientemente avanzata è indistinguibile dalla magia.

• Arthur C. Clarke

La civiltà avanza aumentando il numero di operazioni che possiamo compiere senza pensarci.

• Alfred North Whitehead

L'ho reso più lungo del solito, soltanto perché non ho avuto il tempo di farlo più breve.

• Blaise Pascal

La privacy è il potere di rivelarsi al mondo in modo selettivo.

• Un manifesto Cypherpunk

Il futuro è già qui, semplicemente non è ancora equamente distribuito.

• William Gibson

Tecnologie magiche, progresso della civiltà, brevità di espressione, privacy e un futuro già presente. Ecco, in sintesi, cosa sono le Zero Knowledge Proofs. Ma di cosa stiamo realmente parlando?

Nell'ultimo secolo, computer e internet hanno conquistato il mondo. Queste tecnologie sono ovunque, in tutto quello che facciamo, nel bene e nel male. Su queste fondamenta abbiamo costruito piattaforme, aziende e veri e propri imperi. Parliamo dei giganti MAMAA (Microsoft, Apple, Meta, Alphabet, Amazon). Poi c'è il cuore pulsante del sistema: reti di pagamento, servizi governativi e una miriade di applicazioni B2B che regolano silenziosamente il mondo. Infine, troviamo una moltitudine di altre piccole realtà: app divertenti per modificare immagini, piattaforme per imparare lingue straniere o comunità online.

Quando inserisci dei dati in un qualsiasi servizio online, ti aspetti di ottenere qualcosa in cambio. Può trattarsi di un piccolo obiettivo, come contattare un amico o distrarti dal lavoro, oppure di qualcosa di importante come richiedere un mutuo. Ma che fine fanno davvero questi dati? Non parliamo solo di quelli di cui sei consapevole, ma anche della montagna sommersa di informazioni nascoste. Ciò che desideri accadrà davvero, o ci saranno delle complicazioni, magari oggi o fra un anno?

Chi comprende realmente questi sistemi e le conseguenze del nostro utilizzo? E soprattutto, in che modo questi sistemi utilizzano noi? Certamente qualcuno ne avrà una comprensione maggiore, ma nessuno li conosce tutti fino in fondo, né tantomeno riesce a prevedere come interagiranno, generando conseguenze impreviste.

Come può reagire una persona? Fidandosi. Ma di chi? E perché?

È un problema complesso. Il nostro cervello non si è evoluto per gestire questioni simili. Internet, pur avendoci connesso e semplificato la vita in tanti modi, ha anche creato un discreto caos. In passato, se avevi una conversazione privata, il vento disperdeva le tue parole. Se restavi chiuso fuori casa, chiamavi un fabbro, o al limite forzavi la serratura. Ma con chi parli quando resti escluso dal tuo account Google davanti alla scritta "Accesso negato"? Con nessuno. Ti trovi davanti a un castello invisibile e impenetrabile.

Le ZKPs possono aiutarci. Magari non sempre, non ovunque, e forse non proprio in questo preciso momento. Ma già oggi possono essere applicate in numerosi contesti, e in futuro lo saranno sempre di più. Nel resto di questo articolo cercherò di convincerti del perché e del come. Seguiamo insieme questa magia.

---

Cos'è una Zero Knowledge Proof?

Questa sezione introduce il concetto di Zero Knowledge Proof

Questo è il primo di una serie di articoli sulle Zero Knowledge Proofs e le loro applicazioni. Vedremo cosa sono le Zero Knowledge Proofs, perché dovrebbero interessarci, come funzionano e dove possono essere utilizzate.

Immagina di entrare in un bar e dimostrare di avere più di 18 anni senza rivelare nient’altro, nemmeno il tuo documento con tutte le informazioni personali. Oppure immagina di poter dimostrare di aver pagato correttamente le tasse, senza rivelare dettagli sul tuo reddito o patrimonio. Questi sono esempi concreti di ciò che le Zero Knowledge Proofs (ZKPs) permettono di fare. Il termine zero knowledge ("conoscenza zero") indica semplicemente che non viene rivelata alcuna informazione al di là di quella strettamente necessaria.

Le ZKPs consentono di dimostrare che un’asserzione (statement) è vera senza rivelare nient’altro.

Ma cosa significa in pratica? Consideriamo il classico esempio di "Dov’è Wally". Lo scopo del gioco è trovare Wally in un’immagine grande e affollata. Posso dimostrarti di sapere esattamente dov’è Wally senza rivelarti la sua posizione. Ma come?

Immagina di avere l’immagine di "Dov’è Wally" e un grande foglio di carta, quattro volte più grande dell’immagine stessa. Pratico un piccolo foro nella carta e poi la sovrappongo con cura all’immagine, in modo che Wally sia visibile soltanto attraverso quel foro. In questo modo tu riesci a vedere Wally, ma soltanto lui e nient’altro. Così facendo, capisci che io conosco davvero la posizione di Wally, senza però rivelarti il punto esatto in cui si trova nell’immagine.

Ovviamente questo è soltanto un esempio giocattolo, ma speriamo possa offrire un’intuizione di come una simile dimostrazione sia possibile. Che cosa stiamo provando, esattamente? E cosa significa questo concretamente? Lo approfondiremo in seguito. Per ora, vediamo più in generale cosa ci permettono le ZKPs.

Le ZKPs consentono di dimostrare affermazioni arbitrarie in modo molto generale. Più nello specifico, permettono di dimostrare qualcosa in modo privato e sintetico.

Come vedremo tra poco, questa caratteristica è incredibilmente potente.

Perché dovrebbero interessarti?

Questa sezione spiega perché qualcuno potrebbe interessarsi alle ZKPs, approfondendo aspetti come privacy, compressione e la loro natura general-purpose.

Dopo aver letto la sezione precedente potresti pensare: "Va bene, carino, ma perché dovrebbe interessarmi?". È una reazione più che comprensibile. Anzi, forse non dovrebbe interessarti affatto! Esattamente come potrebbe non interessarti sapere come funzionano i computer, dove ci porterà l’intelligenza artificiale o argomenti simili.

Perché allora potrebbe interessarti? Magari perché sei curioso e vuoi capire come funzionano le ZKPs e quali nuove interazioni possono abilitare. Si tratta di un meccanismo molto generale, e per molte persone che lavorano in questo settore rappresenta un paradigma completamente nuovo, capace di aprire le porte a moltissime possibilità ancora inesplorate. È qualcosa che sta già avvenendo, e sembra proprio che siamo soltanto agli inizi. Nel resto di questa sezione proverò a darti qualche intuizione sul perché e sul come.

Prima di entrare più nel dettaglio, cerchiamo di capire cosa ci offrono le ZKPs ad alto livello. Le ZKPs garantiscono principalmente una o entrambe queste proprietà:

1. Privacy (formalmente nota come conoscenza zero, zero-knowledge)

2. Compressione (formalmente nota come sinteticità, succinctness)

Ma cosa intendiamo esattamente con questi due concetti? Ecco alcuni esempi per comprenderli meglio queste proprietà.

Privacy

Ci sono tante cose che desideriamo mantenere private. Ecco la definizione di "privato" secondo l’Oxford Dictionary:

appartenente o destinato esclusivamente all'uso di una determinata persona o gruppo di persone.

Abbiamo conversazioni private, bagni privati, parti intime (private). Segreti aziendali, informazioni personali sensibili, la privacy della nostra casa. Chiavi, porte e serrature.

La privacy è qualcosa di normale che ci accompagna ogni giorno. È strettamente collegata a concetti come sovranità personale, autodeterminazione e indipendenza. Questi principi sono così radicati nella nostra cultura che documenti fondamentali come la Carta dei Diritti degli Stati Uniti e lo Statuto delle Nazioni Unite li riconoscono come diritti essenziali per individui e nazioni. ¹ La privacy è un presupposto fondamentale per la libertà.

In termini più formali, la proprietà della privacy nelle ZKPs viene spesso indicata come zero knowledge (conoscenza zero) o data hiding (occultamento dei dati). ² Una ZKP nasconde i dati non essenziali al funzionamento di un’applicazione, vincolandoli (bound) esclusivamente ai dati rilevanti per quella specifica applicazione. Questi concetti sono più formali e tecnici, e consentono di garantire la privacy. Dato però che quest'ultima è un concetto più ampio e versatile, per ora continueremo a concentrarci principalmente su di essa.

Nel mondo digitale, chiamato anche cyberspazio (in contrapposizione allo spazio fisico, detto meatspace), la privacy è altrettanto essenziale, anche se spesso trascurata. Ecco la definizione di privacy fornita da A Cypherpunk's Manifesto:

La privacy è il potere di rivelarsi al mondo in modo selettivo.

• A Cypherpunk's Manifesto ³

Conversazioni, password, informazioni delle carte di credito. Questi sono esempi di ciò che desideriamo mantenere privato quando siamo online. Internet è uno strumento straordinario che ci connette tutti, ma è anche un mare aperto e pericoloso. Ci sono molti estranei e malintenzionati, e mantenere private certe informazioni è vitale. Senza privacy, attività quotidiane come lo shopping online o la messaggistica privata sarebbero impossibili.

Potresti pensare: "Possiamo già mantenere private informazioni come le password, dov'è la novità?". In un certo senso, hai ragione per questi esempi specifici. Dobbiamo però sforzarci di immaginare qualcosa di più per capire fino in fondo quali possibilità apra la privacy programmabile di tipo general-purpose.

Ad esempio, considera come Agostino, nelle sue Confessioni (400 d.C.), trovasse insolito il fatto che il vescovo Ambrogio praticasse la "lettura silenziosa". All'epoca era normale leggere ad alta voce. ⁴

Quando [Ambrogio] leggeva, gli occhi percorrevano le pagine e il cuore ne coglieva il significato, ma la voce taceva e la lingua restava immobile. Chiunque poteva avvicinarsi liberamente, e gli ospiti non venivano comunemente annunciati. Spesso quindi, quando andavamo a trovarlo, lo sorprendevamo assorto in silenzio in tale lettura, poiché non leggeva mai ad alta voce.

Oggi diamo per scontata la lettura silenziosa, al punto da non riuscire quasi a immaginare che sia stato necessario inventarla. In passato, l’idea che ciò che si leggeva potesse essere riservato esclusivamente ai propri occhi era qualcosa di estraneo. Quali altre invenzioni simili potranno emergere nella nostra epoca moderna? Cose che attualmente la maggior parte di noi non riesce neanche lontanamente a immaginare.

Nelle prossime sezioni daremo uno sguardo a come potrebbero apparire queste invenzioni basate sulle ZKPs, sia quelle già esistenti, sia quelle che emergeranno in futuro.

Compressione

L'ho reso più lungo del solito, soltanto perché non ho avuto il tempo di farlo più breve.

• Blaise Pascal ⁵

La definizione di comprimere qualcosa è:

spingere qualcosa in uno spazio più piccolo

Allo stesso modo, la sinteticità è definita come:

the act of expressing something clearly in a few words

l'atto di esprimere qualcosa in modo chiaro e conciso

Quando diciamo che le ZKPs possiedono la proprietà di compressione, intendiamo dire che è possibile dimostrare la veridicità di qualcosa con una dichiarazione molto breve (succinct). Ad esempio, possiamo dimostrare che tutti i passaggi di un certo calcolo sono stati eseguiti correttamente. Questo è particolarmente utile quando una risorsa è molto richiesta e costosa. È il caso della blockchain di Ethereum, ma si tratta di una proprietà utile anche in molti altri contesti. Ancora più notevole è il fatto che la dimensione della prova rimanga invariata indipendentemente dalla complessità di ciò che vogliamo dimostrare!

Cosa intendiamo con "prova" e "dimensione della prova"? Si tratta di concetti matematicamente ben definiti e ricchi di sfumature. Nelle prossime sezioni approfondiremo meglio cosa significa una "prova" nel contesto delle ZKPs. Per ora, possiamo considerarla semplicemente come una dichiarazione breve che sappiamo essere vera, o che possiamo in qualche modo verificare come tale.

In un classico giallo alla Sherlock Holmes, il detective raccoglie indizi finché non riesce a dimostrare con certezza chi sia l’assassino. Nel gran finale, espone esattamente come è arrivato a questa conclusione. Possiamo considerare questa dichiarazione finale come la "prova". ⁶

In termini più tecnici, questa proprietà si chiama succinctness (sinteticità). ⁷ È ciò che consente alla prova di mantenere la stessa dimensione indipendentemente dalla complessità di ciò che vogliamo dimostrare. Nel contesto delle blockchain pubbliche, questa proprietà è legata anche al concetto di scalabilità. In blockchain come Ethereum, dove lo spazio disponibile nei blocchi è limitato e costoso, le ZKPs possono rendere le transazioni molto più economiche e veloci. Come? Creando una prova che certifichi che un insiemi di transazioni sono avvenute, e registrando solo quella prova sintetica sulla blockchain, anziché l’intero contenuto delle transazioni. Con le ZKPs, questo processo può essere realizzato in modo estremamente sicuro.

La sinteticità è una proprietà generale e indipendente dal concetto stesso di "blockchain": semplicemente, queste ne traggono particolare beneficio per molte ragioni. In generale, avere una prova breve che qualcosa è vero è estremamente utile. Vediamo alcuni punti di vista per capirne meglio il motivo.

Un modo per comprenderlo è pensare ai costi di transazione. ⁸ In generale, più bassi sono, maggiore sarà il valore e la ricchezza che possiamo generare. Se le cose da verificare sono poche, o se verificarle diventa più semplice, possiamo agire con maggiore libertà e facilità.

A volte, quando compiliamo un modulo online, ci viene chiesto di inserire due volte la nostra email per confermare che sia corretta. Questo serve a prevenire errori umani e a rendere più affidabile la trasmissione dei dati. Esistono anche meccanismi come i checksum: una cifra aggiuntiva presente nei codici dei pacchi UPS, nei numeri delle carte di credito o nei codici ISBN dei libri, che funziona come un semplice controllo per verificare che tutti i numeri inseriti siano corretti. Ovviamente, questi metodi non proteggono da usi malevoli, ma solo da errori involontari. ⁹

Nei file system dei computer, un hash viene spesso usato per garantire l’integrità dei file. Se anche solo una piccola parte del file viene alterata, l’hash cambia completamente. Essendo sintetico (ad esempio, una stringa di 64 caratteri), l’hash è semplice da conservare e verificare anche se il file originale è molto grande. In questo caso, le funzioni hash garantiscono l’integrità in modo sicuro. Se invece verificassimo l’integrità di un file conservandone una copia completa, il processo sarebbe estremamente inefficiente. Che il file sia grande o piccolo non importa: l’hash mantiene sempre la stessa dimensione. È proprio la sinteticità dell’hash a rendere possibile tutto questo.

Che cosa sai?

Facciamo un passo indietro rispetto a compressione, sinteticità e prove. Prendiamoci una breve deviazione per parlare di conoscenza, carico cognitivo e fiducia. Alla fine della sezione, collegheremo tutto questo di nuovo alle ZKPs.

Nella vita quotidiana, cosa sai essere vero e perché? Se vedi il sole sorgere ogni giorno, probabilmente ti aspetti che sorga anche domani. Nel mondo moderno siamo perlopiù protetti dalle avversità della natura, ma al contempo dobbiamo affrontare altre preoccupazioni, più moderne. Molte di queste hanno a che fare con le istituzioni con cui interagiamo ogni giorno.

Se riesci a prelevare contanti dalla tua banca ogni giorno, ti aspetti di poterlo fare anche domani? La maggior parte delle persone probabilmente direbbe di sì, ma non è sempre così per tutti. Dipende da molti fattori: dall'affidabilità della banca, dalla stabilità del paese in cui vivi, da eventuali eventi rilevanti nell’economia globale, o dalla tua situazione personale. Tutti questi elementi forniscono indizi, e su quella base prendi una decisione.

Questo è ovviamente un esempio banale, ma la vita ne è piena. Tutto ciò può essere visto come una forma di carico cognitivo. Quanto questo incida dipende dalla tua situazione personale e dalla complessità delle tue interazioni quotidiane. Per esempio, un’azienda prenderà in seria considerazione questi fattori quando stipula un contratto con un’altra parte.

Creiamo meccanismi e regole per gestire questa incertezza: servizi di reputazione, audit indipendenti, sanzioni per scoraggiare comportamenti scorretti, richiesta di accreditamento presso alcune istituzioni fidate, ecc. Tutte queste misure sono in sostanza dei cerotti, tentativi di arrivare al cuore del problema. È davvero ciò che dichiara di essere? Rispetta le regole che abbiamo stabilito? È affidabile e utilizzabile?

Questo carico cognitivo aumenta drasticamente quando si interagisce con più istituzioni, giurisdizioni, aziende e persone. Possono verificarsi effetti a catena: la tua banca fallisce, non riesci a pagare i dipendenti, e di conseguenza la tua attività non riesce a servire i clienti. ¹⁰ Servono più controlli. Più momenti per chiedersi se tutto stia funzionando e cosa potrebbe andare storto.

Concludo questa sezione con una citazione:

La civiltà avanza aumentando il numero di operazioni che possiamo compiere senza pensarci.

• Alfred North Whitehead ¹¹

Per esempio, quando accendi il fornello per cucinare, non devi nemmeno pensare a come accendere un fuoco. È ben diverso dal dover raccogliere la legna, mantenerla asciutta, accendere la fiamma e tenerla viva: un processo lungo e faticoso. In matematica, senza il calcolo infinitesimale, non saremmo mai andati sulla Luna.

Grazie alle ZKPs e alle prove sintetiche, possiamo introdurre maggiore certezza e trasparenza in sistemi opachi. Questo diventa ancora più potente quando consideriamo la composizione delle ZKPs: ovvero la possibilità di combinare più prove in una sola, ad esempio tramite aggregazione o ricorsione.

Tutto ciò presuppone che almeno alcune delle regole o dei meccanismi citati, spesso confusi e incoerenti, possano essere tradotti in una forma comprensibile alle ZKPs. Come possiamo riuscirci?

General-purpose

Ricordiamo che le ZKPs ci permettono di dimostrare asserzioni arbitrarie in maniera general-purpose (generica). Perché questo è importante e in che modo rappresenta un vantaggio?

La differenza tra strumenti esistenti simili e le ZKPs è paragonabile alla differenza tra una calcolatrice e un computer. Una è pensata per svolgere un compito molto specifico, l’altro è general-purpose. È la differenza tra questa macchina calcolatrice ¹² e un computer moderno:

Ricorda gli esempi specifici che abbiamo usato prima per rappresentare in modo concreto privacy e sinteticità. Una password è un'informazione privata che ti permette di accedere a un servizio ¹³. Nel caso di un hash di un dato in ingresso, come un file, ci offre invece un riferimento sintetico per verificarne l’integrità.

Possiamo rappresentare graficamente una funzione di hash in questo modo:

Applichiamo una specifica funzione di hash, come SHA256 ¹⁴, su un dato noto. Ad esempio, usando come input la frase "The quick brown fox jumps over the lazy dog" (senza virgolette) e applicando la funzione SHA256, otteniamo l’hash d7a8fbb307d7809469ca9abcb0082e4f8d5651e46d3cdb762d02d0bf37c9e592. Basta aggiungere un semplice punto alla fine della frase per ottenere un hash completamente diverso: "The quick brown fox jumps over the lazy dog." produce ef537f25c895bfa782526529a9b63d97aa631564d5d789c2b765448c8635fb6c.

Anche se la frase cambia solo di poco, gli hash risultanti sono completamente diversi ¹⁵. Le funzioni di hash sicure sono difficili da “rompere” e possiedono proprietà interessanti. Ad esempio, dato un hash non si può risalire all’input originale. Inoltre, non è facile costruire un messaggio che produca un hash specifico prestabilito. Queste funzioni sono dette funzioni di hash crittografiche ¹⁶.

La funzione SHA256 usata nell’esempio è una funzione crittografica di hash specifica, il cui sviluppo ha richiesto molto tempo e sforzi collettivi. Ma l’hash in sé non dimostra nulla. Ha senso solo se confrontato con qualcos’altro, come l’accesso diretto al messaggio o al file originale.

In modo informale, possiamo considerare una funzione di hash come una prova che un certo messaggio corrisponde a un dato hash. Ma possiamo verificarlo solo conoscendo il messaggio originale. A volte, le persone usano questa tecnica per dimostrare in anticipo di aver scritto qualcosa e fare previsioni. Ad esempio, potrebbero scrivere la frase: "Il 1° aprile 2040, gli alieni atterreranno sul Big Ben a Londra e il numero 25742069 vincerà la lotteria", per poi pubblicare l’hash di quel messaggio, ad esempio su Twitter. Se poi si rivelano avere ragione, possono mostrare il messaggio originale e convincere tutti di essere i nuovi Nostradamus.

Al contrario, possiamo rappresentare una ZKP in questo modo:

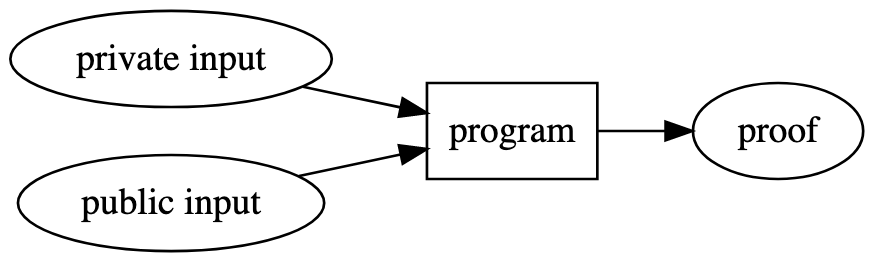
A differenza della funzione di hash vista prima, ci sono alcune differenze fondamentali:

• Possiamo avere più input pubblici e privati, non solo un singolo input pubblico
• Possiamo usare qualsiasi programma, non solo una funzione crittografica di hash
• Otteniamo una prova autosufficiente che può essere verificata

Nel caso dell’hash, dobbiamo rendere pubblico l’input per verificare che corrisponda all’hash. Con le ZKPs invece possiamo anche usare un input privato. L’input privato è qualcosa che solo tu conosci, e che non devi rivelare a nessuno per generare una prova.

Ad esempio, nel caso di "Dov’è Wally" visto all’inizio, l’input pubblico è l’immagine. L’input privato è la posizione di Wally. Posso generare una prova che dimostra che so dove si trova Wally senza rivelarti la posizione.

Allo stesso modo, se ho un Sudoku (un popolare rompicapo logico), posso dimostrarti di conoscere la soluzione senza rivelartela. In questo caso, l’input pubblico è il puzzle iniziale e quello privato è la soluzione.

Avrai notato che "Dov’è Wally" e risolvere un Sudoku sono due problemi molto diversi. Eppure possiamo scrivere un semplice programma che descrive entrambi e usare una ZKP per creare la prova. Questo è possibile perché la logica del programma è general-purpose e può calcolare qualsiasi cosa sia computabile da un computer.

Abbiamo trasformato quello che era un problema di crittografia o matematica (definire e rendere sicura una funzione di hash) in un problema di programmazione. Per capire perchè questo è estremamente potente, considera i seguenti esempi.

Ora possiamo dimostrare di conoscere il dato privato che genera un determinato hash ¹⁷. Questo significa che puoi dimostrare di possedere un certo messaggio, ad esempio un documento importante, senza rivelarne il contenuto.

Per capire meglio la potenza della computazione general-purpose, guardiamo più da vicino le firme di gruppo. Le group signature permettono a più persone di firmare un documento insieme, senza rivelare chi sono. Ad esempio, i Federalist Papers furono firmati dallo pseudonimo "Publius", che rappresentava più autori ¹⁸. Come per la funzione SHA256, è possibile rappresentare le firme di gruppo tramite crittografia e matematica. È un risultato straordinario, frutto di grande ingegneria crittografica. Ma con le ZKPs general-purpose, chiunque può esprimere la stessa cosa con poche dozzine di righe in Circom, un linguaggio di programmaione per scrivere ZKPs ¹⁹.

Grazie alla loro natura generale, possiamo costruire facilmente soluzioni su misura. Ad esempio, potresti avere una carta d’identità con nome, indirizzo e altri dati personali. Per accedere a un evento potresti dover dimostrare di avere più di 18 anni e un biglietto valido. Ma potresti non voler mostrare il tuo indirizzo o rischiare che ti venga rubato il documento. Con le ZKPs puoi dimostrare che:

• Possiedi un documento valido
• Il documento è stato emesso da un ente autorizzato negli ultimi 5 anni
• Il documento non è stato revocato o denunciato come rubato nell'ultimo periodo
• Hai più di 18 anni
• Hai acquistato un biglietto valido per l’evento
• Il biglietto non è già stato usato

Tutto ciò senza rivelare nessuna informazione personale oltre a quelle elencate.

Con le ZKPs ora abbiamo a disposizione uno strumento migliore per coordinare persone e sistemi, soprattutto in contesti dove servono privacy e sinteticità. Vedremo altri esempi nella sezione dedicata alle applicazioni.

Spesso, il limite di ciò che puoi esprimere è solo la tua immaginazione.

Perché proprio ora?

Perché le ZKPs stanno diventando così rilevanti proprio adesso? Ci sono motivi sia tecnici che sociali.

Dal punto di vista tecnico, le ZKP sono relativamente recenti: matematicamente esistono soltanto da poche decine d’anni ²⁰. Proprio come l’informatica, ci è voluto del tempo perché diventassero efficienti e praticabili anche solo in teoria ²¹.

Successivamente, qualcuno ha dovuto trasformare quei paper e quei protocolli crittografici in qualcosa di pratico. Il primo esempio degno di nota è stato Zcash, la criptovaluta orientata alla privacy, lanciata nel 2016. Il progetto nacque da un paper scritto da cypherpunk e ricercatori ²². La versione iniziale fu un’impressionante opera di ricerca e ingegneria applicata a un prodotto reale: pur con molte criticità e ben lontana dall’essere ottimale, fu la prima dimostrazione pratica che le ZKP potevano funzionare nel mondo reale. Da lì è esplosa la ricerca e lo sviluppo in questo campo, soprattutto negli ultimi anni.

Le blockchain pubbliche come Ethereum e Zcash, una criptovaluta orientata alla privacy, hanno avuto un ruolo fondamentale in questo. Le blockchain eccellono in caratteristiche come la resistenza alla censura e la trasparenza ²³. Questi vantaggi, però, comportano un sacrificio in termini di privacy e scalabilità, i punti di forza delle ZKP; da qui la loro naturale combinazione. A ciò si aggiunge la forte propensione della community blockchain verso la crittografia avanzata ²⁴, e non sorprende che molta dell’innovazione si stia concentrando proprio nell’intersezione tra blockchain e ZKPs ²⁵. Grazie ai numerosi progetti blockchain ben finanziati, questo ha portato nuovi investimenti in ricerca e sviluppo in un ambito storicamente più accademico.

Considerando la complessità in gioco, che spazia tra matematica applicata, crittografia, articoli su sistemi ZKP specifici, implementazione di nuovi sistemi di prova, strumenti di sviluppo e applicazioni che vanno a toccare altri domini complessi, i progressi sono rapidissimi. Ogni anno, persino ogni mese, vengono pubblicati nuovi articoli con tecniche inedite, strumenti migliori e nuove applicazioni. Il ciclo tra ricerca, implementazione e utilizzo si stringe sempre di più. Anche se resta difficile, iniziare oggi è molto più facile di qualche anno fa. E man mano che gli strumenti migliorano, agli sviluppatori è richiesto di comprendere sempre meno la matematica che sta alla base delle ZKPs.

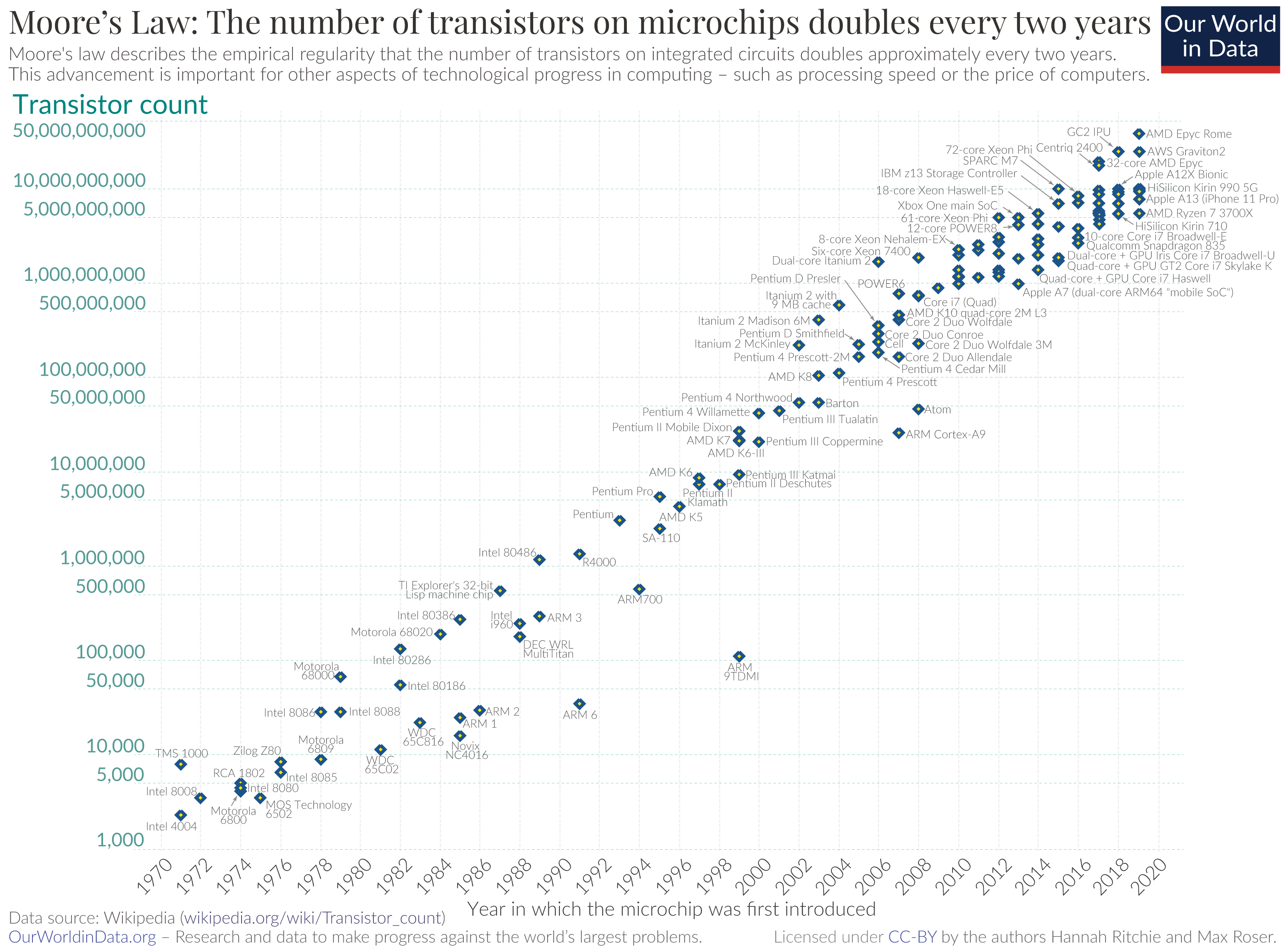
In termini di prestazioni, nel mondo delle ZKPs sta avvenendo una sorta di legge di Moore. La legge di Moore osserva che il numero di transistor raddoppia circa ogni due anni. Questo è ciò che ha reso possibile la rivoluzione informatica. Nelle ZKPs, progetti che pochi anni fa sembravano pura fantascienza, sono oggi eseguiti su cose come zkVM e zkML. In linea di massima, si è osservato che i progressi nel campo delle ZKPs migliorano di un ordine di grandezza ogni anno circa ²⁶. Questo perché si tratta di una tecnologia nuova, in cui è possibile ottimizzare in modo aggressivo su ogni livello dello stack: dai programmi che scriviamo, ai sistemi che usiamo, fino all’hardware stesso. Non abbiamo motivo di credere che questa tendenza si fermerà a breve.

Come funziona?

Questa sezione spiega a grandi linee come funzionano le Zero Knowledge Proofs

Questa sezione fornisce una panoramica generale sul funzionamento delle ZKPs. Non conterrà né matematica, né codice.

Concetti fondamentali

Iniziamo introducendo un po' di terminologia. Ci saranno alcuni termini nuovi da imparare, ma li padroneggerai rapidamente strada facendo.

• Protocollo: sistema di regole che definisce la condotta corretta da seguire
• Prova (Proof): argomentazione che dimostra la verità di un’asserzione
• Dimostratore (Prover): colui che dimostra o prova qualcosa
• Verificatore (Verifier): colui che verifica la correttezza di un’asserzione
• Input privato: input che soltanto il prover può vedere, spesso chiamato witness (informazione privata utilizzata nella dimostrazione)
• Input pubblico: input che sia prover che verifier possono vedere, spesso chiamato instance (istanza)

Pur essendo utile apprendere la terminologia tecnica, a volte le metafore aiutano a capire meglio cosa sta succedendo. Introdurremo ulteriori termini man mano che procediamo.

I protocolli esistono ovunque e possono essere impliciti o espliciti. Negli scacchi, il protocollo prevede che ci siano due giocatori che effettuano mosse a turno seguendo le regole fino alla fine della partita, finchè uno vince o si raggiunge una situazione di parità. In teoria il tempo impiegato per ogni mossa non conta, ma in pratica si cerca di ridurre al minimo i costi di comunicazione fra i due giocatori. Potremmo quindi immaginare una partita a scacchi rapidissima.

Possiamo immaginare Sherlock Holmes come il prover (dimostratore), che nella sua dichiarazione finale presenta una serie di argomentazioni eleganti, ovvero una prova (proof), per dimostrare chi sia l'assassino. Questa prova deve poi essere verificata da un verificatore (verifier), ad esempio un giudice o una giuria, oltre ogni ragionevole dubbio ²⁷. Il dimostratore, in questo caso Holmes, produce la prova; poiché è autosufficiente, chiunque può agire da verificatore, incluso tu lettore, che devi esserne convinto per rendere la storia credibile. ²⁸

L'input privato potrebbe essere una conoscenza esclusiva di Sherlock Holmes, ad esempio un'informazione segreta sussurratagli da qualcuno. Questo tipo di informazione è spesso chiamata witness, il che può generare confusione perché richiama il concetto di testimone in tribunale, che possiede informazioni private aggiunte poi al cumulo di prove. Nel caso delle ZKPs, quest'informazione privata non verrebbe condivisa con il verificatore (verifier), ovvero con il giudice e la giuria nel nostro esempio.

Le ZKPs stabiliscono un protocollo tra un dimostratore (prover) e un verificatore (verifier). Tale protocollo è non interattivo se prover e verifier non hanno bisogno di comunicare direttamente, come avviene invece in una partita di scacchi o in una danza. Invece, il prover produce una singola prova autosufficiente, che viene verificata successivamente. La maggior parte delle ZKPs iniziano come interattive, cioè richiedono uno scambio continuo, ma poi vengono utilizzati alcuni trucchi matematici per renderle non interattive ²⁹. Puoi immaginare la non interattività come due giocatori di scacchi che, dopo poche parole, sanno esattamente quali mosse giocherà l'altro, al punto da non iniziare nemmeno la partita perché conoscono già come finirà.

Esistono molte tipologie di ZKPs. Spesso parliamo di zk-SNARKs, acronimo di Zero Knowledge Succinct Non-Interactive ARguments of Knowledge. Zero Knowledge e Succinctness corrispondono rispettivamente alla privacy e alla compressione descritte sopra. La non interattività è già stata menzionata. "ARguments of knowledge" corrisponde sostanzialmente a una prova (proof) ³⁰. Anche di zk-SNARKs ne esistono numerose varianti.

Un buon modello mentale è pensare alle ZKPs come a uno zoo. Ci sono molti animali diversi e possiamo classificarli in vari modi: questi hanno quattro zampe, questi altri hanno strisce, questi li ha portati Bob l’anno scorso ³¹, ecc. Alcune categorie sono più utili di altre. Infatti, alcuni di questi sistemi non possiedono nemmeno la proprietà di Zero Knowledge! Questi vengono chiamati semplicemente SNARKs. Come comunità, chiamiamo spesso questo variegato insieme di animali semplicemente ZK, anche se molti sistemi in realtà non sfruttano la proprietà Zero Knowledge. ³²

Protocollo

Tornando al nostro protocollo, abbiamo un prover (dimostratore) e un verifier (verificatore). Il prover genera una prova usando una prover key, l’input privato e l’input pubblico. Il verifier verifica la prova utilizzando una verification key e l’input pubblico, e restituisce come risultato true o false.

Abbiamo introdotto due nuovi concetti: la prover key e la verifier key. Queste consentono al prover e al verifier di compiere la loro magia. Puoi immaginarle come chiavi normali che permettono di entrare in un luogo e svolgere un'azione, oppure come bacchette magiche che abilitano determinate operazioni. Queste chiavi derivano da una cerimonia speciale chiamata setup, una fase iniziale di preparazione su cui non entreremo nei dettagli in questo articolo ³³.

Nota che solo il prover ha accesso all’input privato. In che modo il prover utilizza la prover key, l’input privato e quello pubblico per generare una prova?

Ricorda l’illustrazione precedente di una ZKP:

Abbiamo un programma speciale (formalmente chiamato circuit) che codifica la logica di interesse per l’utente. Per esempio, potrebbe dimostrare di conoscere i dati che generano un determinato valore di hash. Diversamente da un normale programma per computer, questo programma è composto da vincoli (constraints) ³⁴. La prova consiste nel dimostrare che tutti questi vincoli vengono soddisfatti insieme al dato input privato e pubblico.

Alla fine, il verifier unisce la prova, la verification key, l’input pubblico e il circuito di vincoli; se tutto torna oltre ogni ragionevole dubbio, restituisce "true", altrimenti "false".

Questa visione è leggermente semplificata, ma coglie l’essenza di quello che sta accadendo.

Vincoli

Cosa sono questi vincoli (constraints) che compongono il programma speciale di cui abbiamo parlato sopra? Un vincolo è una limitazione o una restrizione. Ad esempio, “un numero compreso tra 1 e 9” è un vincolo. Il numero 7 soddisfa questo vincolo, mentre il numero 11 no. Come si scrive un programma sotto forma di vincoli? Questa è una vera e propria arte, ma partiamo con un esempio semplice: il Sudoku.

Nel Sudoku l’obiettivo è trovare una soluzione per una griglia che soddisfi alcuni vincoli. Ogni riga deve contenere i numeri da 1 a 9 esattamente una volta. Lo stesso vale per ogni colonna e per ciascun quadrante 3x3. Viene fornita una configurazione iniziale parziale e il nostro compito è completarla soddisfacendo tutti questi vincoli. La parte difficile sta nel trovare dei numeri che soddisfino contemporaneamente tutti i vincoli.

Con le ZKPs, il prover può costruire una prova (proof) che dimostri di conoscere la soluzione di un determinato rompicapo. In questo caso, la dimostrazione utilizza come input pubblico la configurazione iniziale della griglia e come input privato la soluzione completa, insieme a un circuito (circuit). Il circuito è costituito da tutti i vincoli che esprimono le regole del rompicapo.

Viene chiamato circuito perché questi vincoli sono correlati fra loro e vengono "collegati" insieme, un po’ come in un circuito elettrico. In questo caso il circuito non gestisce corrente elettrica, ma valori. Ad esempio, non possiamo inserire valori arbitrari come “banana” nel vincolo di riga: deve essere un numero compreso fra 1 e 9.

Il verifier possiede lo stesso circuito e lo stesso input pubblico e può verificare la prova ricevuta dal prover. Se la prova è valida, il verifier sarà convinto che il prover abbia realmente una soluzione al rompicapo.

Risulta che molti problemi possano essere espressi come un insieme di vincoli. Infatti, qualsiasi problema risolvibile da un computer può essere espresso come un insieme di vincoli.

Esempio con il Sudoku

Applichiamo ora quanto abbiamo imparato sulle varie componenti di una ZKP all’esempio del Sudoku.

Per il Sudoku, il nostro programma speciale, ovvero il circuito, prende in ingresso due input:

• Un puzzle Sudoku come input pubblico
• Una soluzione al Sudoku come input privato

Il circuito è composto da una serie di vincoli. Tutti questi vincoli devono essere soddisfatti contemporaneamente. I vincoli sono i seguenti:

• Tutte le cifre nel puzzle e nella soluzione devono essere comprese tra 1 e 9
• La soluzione deve corrispondere al puzzle in tutti i punti in cui le cifre erano già state inserite
• Tutte le righe devono contenere le cifre da 1 a 9 esattamente una volta
• Tutte le colonne devono contenere le cifre da 1 a 9 esattamente una volta
• Tutti i quadranti devono contenere le cifre da 1 a 9 esattamente una volta

Se tutti questi vincoli sono soddisfatti per un puzzle e la sua soluzione, sappiamo che la soluzione è valida.

Una dimostratrice (prover) chiamata Peggy usa la sua prover key, il puzzle e la soluzione, li combina con il circuito speciale e genera una prova (proof). La prova è brevissima, meno di 1000 caratteri, ed è autosufficiente: contiene tutto ciò che serve al verificatore (verifier) per controllarla. Puoi pensarla come una formula magica che fa esattamente ciò che desideri, senza che tu debba capirne i dettagli ³⁵.

Ecco una formula magica tratta da un libro di incantesimi, scritto da un medico gallese nel XIX secolo:

Ecco invece un esempio reale di Zero Knowledge Proof generata dalla libreria Circom/snarkjs:

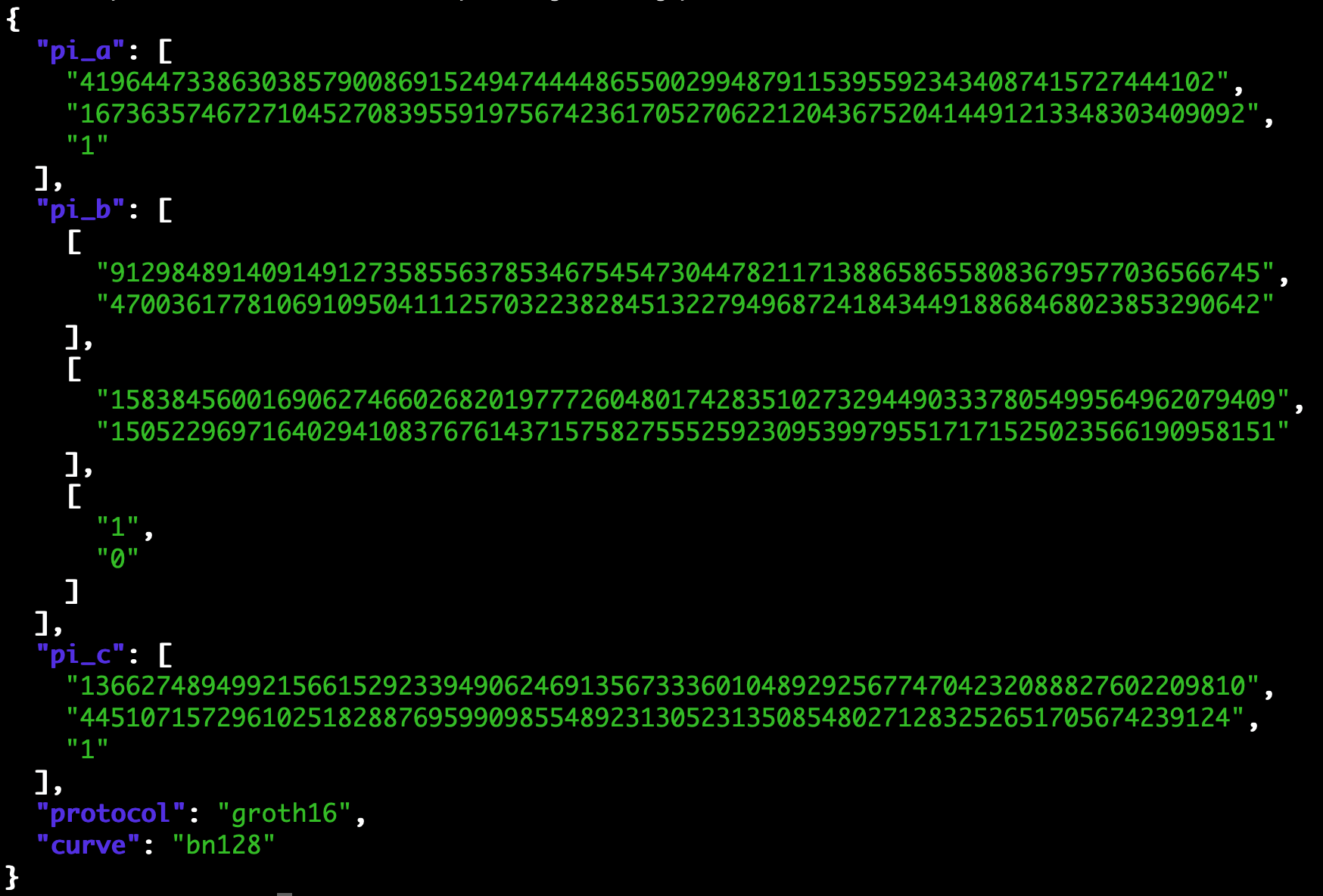
Solo che in questo caso, la magia funziona davvero.

Victor, il verificatore, usa la sua verifier key e il puzzle originale per controllare che la prova inviata da Peggy sia corretta. Se lo è, l’output sarà true; altrimenti false. La magia o funziona o non funziona, non c’è via di mezzo. Così Victor è certo che Peggy conosce la soluzione a quel specifico problema, senza averla mai vista. Et voilà ³⁶

Alcune proprietà

Diciamo che una ZKP possiede alcune proprietà tecniche fondamentali:

• Completezza (Completeness): se l’asserzione è vera, allora il verifier sarà convinto dalla prova.
• Solidità (Soundness): se l’asserzione è falsa, il verifier non sarà convinto dalla prova, tranne che con una probabilità trascurabile.
• Conoscenza zero (Zero Knowledge): se l’asserzione è vera, non verrà rivelato nulla oltre al fatto che sia vera.

Inoltre, nel caso degli zk-SNARKs, la prova è succinta (succinct), il che significa che non aumenta di dimensione anche quando il programma diventa più complesso ³⁷.

Ci sono anche altre proprietà che consideriamo importanti nel caso pratico delle ZKPs:

• Quali ipotesi matematiche fa il sistema?
• Quanto è sicuro?
• Richiede una trusted setup (fase iniziale fidata per generare parametri di sistema)?
• Quanto è complesso generare la prova, in termini di tempo e risorse?
• Quanto è complesso verificare la prova, in termini di tempo e risorse?
• Il sistema ZKP permette di aggregare o combinare più prove tra loro?
• Esistono buone librerie per un determinato sistema ZKP che possono essere usate dagli sviluppatori?
• Quanto è espressivo il linguaggio utilizzato per scrivere programmi per un determinato sistema ZKP?
• E così via.

Come puoi vedere, ci sono molte considerazioni da fare e numerose varianti di ZKPs. Non preoccuparti troppo però, perchè il concetto di base rimane sempre lo stesso, e a seconda dei tuoi interessi puoi tranquillamente ignorare molti dettagli tecnici. Tornando alla metafora dello zoo, non è necessario diventare biologi, potresti voler lavorare solo con alcuni animali, adottarne uno oppure semplicemente accarezzare il cane di un amico.

Applicazioni

Questa sezione fornisce esempi di applicazioni presenti e future delle ZKPs

Ci sono molte applicazioni delle ZKPs. In generale, siamo ancora nelle fasi iniziali. Gran parte dell’attenzione è rivolta ai protocolli e all’infrastruttura sottostante, così come alle applicazioni specifiche della blockchain. Per apprezzare meglio gli esempi specifici della blockchain è utile avere qualche nozione sul funzionamento delle blockchain pubbliche e sui problemi che esse affrontano. Questo, però, non è un prerequisito obbligatorio. In questa sezione esamineremo alcune delle applicazioni più interessanti. Inizieremo con quelle già attive oggi e poi esploreremo quelle che si intravedono all’orizzonte.

Il futuro è già qui. Semplicemente non è ancora distribuito in modo uniforme.

• William Gibson ³⁸

Applicazioni già attive

Contante elettronico (Electronic cash). Per creare sistemi di pagamento online simili al contante fisico, è necessario che siano fungibili e riservati. La fungibilità è la proprietà di un bene di essere sostituibile con un altro identico. In altre parole, non c'è differenza tra il mio denaro e il tuo: entrambi sono forme di pagamento altrettanto valide. Possiamo utilizzare le ZKPs per mantenere privato il grafico delle transazioni, diversamente da quanto avviene in Bitcoin o Ethereum. In questo modo, la tua cronologia delle transazioni rimane privata, garantendo la fungibilità del denaro elettronico. Sistemi di questo tipo sono attualmente attivi con Zcash e servizi analoghi come Tornado Cash ³⁹.

Segnalazione anonima (Anonymous signaling). Spesso è necessario dimostrare la propria appartenenza a un gruppo che possiede certe caratteristiche, senza però rivelare la propria identità. Un esempio è provare che fai parte di un determinato gruppo di persone; un altro è il voto. Ciò significa che non colleghi la tua identità ad azioni sensibili, come dichiarare per quale partito hai votato, né riveli informazioni non necessarie. Attualmente attivo in sistemi come Semaphore ⁴⁰, esistono anche molti altri meccanismi simili con diverse varianti.

ZK Rollup. Permette di effettuare transazioni più numerose, economiche e veloci. Lo spazio della blockchain Ethereum è limitato e costoso, con una domanda molto alta. Si usa allora una soluzione cosiddetta di tipo Layer 2 (L2) rollup, che esegue transazioni separate dalla blockchain principale (L1). Quando un certo numero di transazioni è stato completato sul L2, queste vengono "aggregate" (rollup) e inviate sul L1. Le ZKPs sono ideali perché consentono di (i) dimostrare che le transazioni sono state eseguite correttamente e (ii) creare una prova succinta che occupa poco spazio sul L1. Ciò rende le transazioni più economiche e veloci per gli utenti, con un livello di sicurezza quasi equivalente. A causa della complessità nel dimostrare l’esecuzione completa della Ethereum Virtual Machine (EVM), molte soluzioni di ZK Rollup si concentrano esclusivamente sullo scambio di beni e asset semplici. Sistemi di questo tipo sono già attivi, come Loopring, zkSync Lite, dYdX e Starknet ⁴¹.

ZK-EVM. Simile al concetto di ZK Rollup, ma universale, perché può eseguire qualsiasi tipo di transazione o programma. Ethereum possiede una EVM che funge da computer globale e condiviso per scopi generali (su cui chiunque può scrivere). Implementando la logica di questa macchina utilizzando le ZKPs, è possibile dimostrare l’esecuzione corretta di qualsiasi programma scritto su Ethereum e creare una prova succinta di tale esecuzione. Questo ha diverse applicazioni, soprattutto per migliorare la scalabilità e permettere transazioni più economiche e veloci. Sistemi già attivi comprendono Polygon zkEVM e zkSync Era, con numerosi altri progetti in arrivo ⁴².

ZK-VM. A causa, in parte, della difficoltà di lavorare con una piattaforma poco adatta agli SNARK (snark-unfriendly) ⁴³ come la EVM, molti progetti hanno scelto di creare una blockchain completamente nuova, separata da Ethereum. Ciò consente di ottimizzare la macchina virtuale (VM) direttamente per le ZK. A seconda del sistema specifico, questo permette privacy e verifica succinta dello stato della blockchain. Mina è già attiva, mentre sistemi come Aleo sono in fase di sviluppo. ⁴⁴

Dark Forest. Dark Forest è un gioco strategico in tempo reale con informazione incompleta. I giochi di questo tipo basati su ZK hanno una "nebbia di guerra crittografica" (cryptographic fog of war), in cui i giocatori possono vedere solo una parte limitata del mondo di gioco, restrizione garantita dalle ZK. A differenza dei giochi tradizionali come Starcraft, nemmeno un server centrale può accedere a tutte le informazioni. Grazie alla sua natura programmabile, questo approccio abilita modalità di gioco innovative. ⁴⁵

ZK Bridges. I bridge (ponti) consentono di spostare asset tra blockchain e sistemi diversi. Tali bridge sono spesso difficili da mettere in sicurezza e sono frequentemente oggetto di attacchi hacker. Grazie alle ZK, possiamo trasferire asset in modo più sicuro e veloce, senza affidarci a terze parti fidate o a metodi soggetti a errori. Soluzioni di questo tipo sono già attive con zkBridge, e altri progetti simili sono in fase di sviluppo, come ad esempio Succinct Labs. ⁴⁶

Identità privata (Private identity). Poiché un numero sempre maggiore di sistemi chiusi ospita e richiede le nostre identità online ⁴⁷, è importante che gli utenti possano controllare, aggregare e mantenere private queste identità frammentate. Progetti attualmente attivi come Sismo permettono di ottenere questo risultato, e altri progetti stanno sviluppando sistemi simili. ⁴⁸

Questi sono solo alcuni esempi e non una lista esaustiva. Non abbiamo parlato di altri utilizzi come la reputazione privata e non ripudiabile, l’esportazione della reputazione da Web2, la protezione da attacchi sybil-resistant, prove resistenti alla coercizione, la proof of replication, gli airdrop anonimi, la dimostrazione di gradi di separazione, ecc. ⁴⁹

All'orizzonte

ZK-EVM equivalente a Ethereum (Ethereum-equivalence). Esistono diverse tipologie di ZK-EVM, e quelle più difficili da realizzare sono quelle totalmente equivalenti a Ethereum. Altre ZK-EVM adottano scorciatoie per semplificare la generazione delle prove. Con una ZK-EVM totalmente equivalente a Ethereum, non c'è alcuna differenza rispetto al sistema Ethereum attuale. Ciò permette di dimostrare l’esecuzione corretta di ogni singolo blocco tramite una prova succinta. Potresti addiririttura usare uno smartphone per verificare l'integrità di tutta la blockchain, basandoti esclusivamente sulla matematica, senza necessità di affidarti a terze parti o di utilizzare macchine costose. Attualmente in fase di sviluppo da parte del team ZK-EVM Community Edition. ⁵⁰

Computazione dimostrabile general-purpose (General purpose provable computation). Gran parte delle computazioni al mondo non avviene sulla EVM, bensì su altri sistemi. Programmi basati su WASM e LLVM sono molto diffusi ⁵¹. Possiamo utilizzare lo stesso approccio della ZK-EVM per svolgere computazioni private dimostrabili di uso generale. Ad esempio, è possibile dimostrare che un database contiene un determinato record senza rivelare altre informazioni. Attualmente questa tecnologia è oggetto di sviluppo da parte di diversi team, tra cui Delphinus Labs, RISC Zero, Orochi Network e nil.foundation. ⁵²

ZK Machine Learning (ZK ML). È possibile dimostrare privatamente che una determinata computazione sia stata svolta correttamente fuori dalla blockchain (off-chain), pubblicando successivamente soltanto la prova della sua corretta esecuzione. Questo consente di utilizzare dati privati per addestrare modelli migliori senza rivelare tali dati, ad esempio documenti sensibili, registrazioni vocali o persino sequenze di DNA per individuare problemi di salute. Tutto ciò migliora sia la scalabilità sia la privacy degli utenti. Attualmente esistono prove di concetto (PoC) per applicazioni semplici come MNIST, un noto test usato nel Machine Learning per riconoscere cifre scritte a mano, e si sta lavorando su applicazioni più complesse, come reti neurali implementate nelle ZKPs. ⁵³

Autenticità di foto e video (Photo authenticity). È possibile dimostrare l’origine e l'autenticità di contenuti come foto e video, incluse modifiche standard di post-elaborazione. In altre parole, dimostrare che una foto sia stata scattata in un determinato luogo e momento, e che abbia subito soltanto modifiche basilari come il ridimensionamento, il ritaglio e la conversione in scala di grigi (operazioni approvate dall’agenzia AP). Alcuni progressi sono già stati fatti, compresa una prova di concetto (PoC). ⁵⁴

Conformità normativa (Compliance). È possibile dimostrare che una transazione privata rispetta determinate normative o che un determinato asset non sia incluso in una lista nera. Inoltre, si può dimostrare che una piattaforma di scambio (exchange) è solvibile senza rivelarne gli asset. Alcuni sistemi come Espresso Labs hanno già sviluppato soluzioni in questo ambito, e alcune piattaforme dispongono già di versioni semplificate.

Intenzioni schermate e private. Gli utenti delle blockchain pubbliche hanno spesso obiettivi precisi, che possono essere espressi come intenzioni (intents). Ad esempio, un utente potrebbe voler scambiare un token con un altro. Queste intenzioni possono essere condivise con altri utenti per trovare controparti adatte. È auspicabile che tali intenzioni siano schermate (shielded), cioè nascondano il “chi” ma non il “cosa”, in modo simile alle transazioni schermate di Zcash, oppure completamente private. Attualmente in sviluppo da parte del progetto Anoma, iniziando con un sistema di matching schermato. Rendere completamente privato il matching delle intenzioni richiederà probabilmente avanzamenti significativi nella crittografia, analogamente all’ultimo esempio di questa sezione.

Mondi autonomi (Autonomous worlds). Un’estensione di concetti come Dark Forest. Un "mondo" può essere fisico o concettuale, come il mondo di Narnia, il Cristianesimo, il dollaro statunitense, Bitcoin o il diritto anglosassone (Commonwealth). A seconda dell’ambiente in cui operano, questi mondi possono diventare autonomi se chiunque può modificarne le regole senza comprometterne l’oggettività. Attualmente esplorato dalla 0xPARC Foundation nel contesto dei giochi e della creazione di questi mondi. ⁵⁵

Prova di autenticità dei dati (Proof of data authenticity). Consente di esportare dati da applicazioni web e dimostrare privatamente certe informazioni. Sfrutta il protocollo TLS, funzionando pertanto con qualsiasi sito web moderno. Attualmente in sviluppo da parte di TLSNotary. ⁵⁶

Disarmo nucleare (Nuclear disarmament). Consente agli ispettori di siti nucleari di confermare se un determinato oggetto sia o meno un’arma nucleare, senza dover ispezionare i dettagli sensibili della struttura interna. Sono già stati pubblicati articoli scientifici con simulazioni fisiche in proposito. ⁵⁷

Trattative di pace e negoziazioni ad alto rischio (Peace talks and high-stakes negotiation). Spesso nelle trattative esistono limiti invalicabili che ciascuna parte preferisce non rivelare per non indebolire la propria posizione negoziale. Codificando esplicitamente questi limiti, due parti possono trattare questioni estremamente complesse e giungere a un accordo senza rivelare dettagli specifici dei loro parametri e limiti. Ciò consente a parti che non si fidano reciprocamente di raggiungere accordi fruttuosi. Probabilmente richiederà avanzamenti significativi nella Multi-Party Computation (MPC), che consente calcoli su segreti condivisi. ⁵⁸

Ancora una volta, questa non è una panoramica completa di tutte le idee e progetti attualmente in corso. Sicuramente ne emergeranno molti altri in futuro. Come puoi intuire, ci sono davvero molte possibilità offerte dalla ZK.

Potresti chiederti perché molte di queste applicazioni coinvolgano la blockchain. Questo punto è stato parzialmente chiarito nella sezione precedente "Perché proprio ora?". Le ZK sono una tecnologia ortogonale rispetto alle blockchain come Ethereum e possono essere usate anche senza blockchain, ma spesso quest’ultima rappresenta semplicemente uno strumento utile da sfruttare.

Analogamente, le persone che lavorano a queste applicazioni e i problemi che affrontano sono spesso sovrapponibili. Man mano che il settore maturerà, possiamo aspettarci che il concetto di "blockchain" nelle applicazioni ZK finisca per diventare un semplice dettaglio implementativo, cosa che in parte è già successa. In un futuro ancora più lontano, anche la componente "ZK" potrebbe diventare meno visibile, fino al punto in cui si tratterà semplicemente di un’applicazione che utilizza le ZKP come elemento secondario.

Infine, quando è stata sviluppata la crittografia per la messaggistica online e simili, è stata sfruttata e perfezionata principalmente dai militari e dalle aziende Internet. Non è stato qualcosa di innovato dalle poste o da aziende coinvolte nel trasporto sicuro di beni fisici, anche se teoricamente ciò sarebbe stato possibile. ⁵⁹

Termino questa sezione con una citazione di Barry Whitehat, un noto ricercatore ZK che lavora con il team Privacy and Scalability Explorations (PSE) della Ethereum Foundation, quando gli è stato chiesto di fare previsioni sul futuro delle ZK:

"Entro il 2040, qualcuno avrà vinto il Premio Nobel per la Pace per aver utilizzato le Zero Knowledge Proofs." ⁶⁰

Stravagante e audace? Sicuramente. Accadrà davvero? Forse no. Ma potrebbe? Assolutamente sì. È una prospettiva intrigante da considerare. Qual è la differenza tra il modello mentale di chi la considera una possibilità concreta e quello di chi invece la scarta immediatamente? Cosa dovrebbe accadere affinché tale evento diventi un esito realistico?

Le ZKP rappresentano uno strumento nuovo e incredibilmente potente. Spesso, è solo la nostra immaginazione riguardo alle possibili applicazioni che ci limita.

Conclusione

Questa sezione riassume l’articolo e indica i passi successivi

In questo articolo abbiamo visto cosa sono le Zero Knowledge Proofs, perché vale la pena interessarsene e in quali situazioni risultano utili. Abbiamo analizzato a grandi linee il loro funzionamento, le proprietà che garantiscono e alcune applicazioni, già operative o ancora in fase di sviluppo.

Mi auguro che tutto ciò ti abbia aiutato a comprendere meglio la natura delle ZKPs, magari facendoti vivere qualche momento di illuminazione e ispirandoti nuove prospettive su questi temi. Forse ti aiuterà anche a seguire più da vicino la magia delle ZKPs in futuro.

Nei prossimi articoli, approfondiremo ulteriormente alcuni di questi aspetti e analizzeremo dettagli più tecnici per capire meglio come funzionano le ZKPs e in quali contesti possono essere utilizzate.

Se qualcosa in particolare ha attirato la tua attenzione, o se c’è qualche argomento che vorresti vedere trattato in futuro, non esitare a contattarmi su Twitter o via email. Includerò i commenti migliori come note a piè di pagina!

Ringraziamenti

Grazie a Michelle Lai, Chih-Cheng Liang, Jenny Lin, Anna Lindegren e Eve Ko per aver letto le bozze e aver fornito preziosi suggerimenti.

Un ringraziamento speciale a Silvio Meneguzzo per la traduzione e l’adattamento di questo articolo. Ci auguriamo che questo contenuto sia utile e d’ispirazione per la comunità italiana e per tutti gli appassionati di ZK e crittografia.

Immagini

• Dov'è Wally? - Fonte sconosciuta, Where's Waldo creato originariamente da Martin Handford
• Lettura Silenziosa - Jorge Royan, CC-BY-SA 3.0, tramite Wikimedia Commons
• Sherlock Holmes - Sidney Paget, Pubblico dominio, tramite Wikimedia Commons
• Allunaggio - Neil A. Armstrong, Pubblico dominio, tramite Wikimedia Commons
• Calcolatrice di Pascal - kitmasterbloke, CC-BY 2.0, tramite Openverse
• Legge di Moore - Max Roser, Hannah Ritchie, CC-BY 4.0, tramite Wikimedia Commons
• Sudoku puzzle - Tim Stellmach, CC0, tramite Wikimedia Commons
• Incantesimo - National Library of Wales, CC0, tramite Wikimedia Commons
• Cyberpunk - bloodlessbaron, Pubblico dominio, tramite Openverse

Riferimenti

Footnotes

1. Sebbene i concetti siano collegati, esiste controversia legale sul fatto che il "diritto alla privacy" sia effettivamente tutelato in molte giurisdizioni nel mondo. Vedi la voce Wikipedia sul Right to privacy per approfondire. ↩

2. Il concetto di Zero Knowledge ha una definizione matematica precisa, ma non entreremo nei dettagli in questo articolo. Vedi ZKProof Community Reference per una definizione più rigorosa. ↩

3. Vedi A Cypherpunk Manifesto per il testo completo. Consulta anche Wikipedia sulla voce Cypherpunks. ↩

4. Alcune persone interpretano diversamente questo passaggio specifico, ma è comunque vero che gli esseri umani sono passati dalla narrazione orale alla lettura silenziosa solo in tempi relativamente recenti. Vedi Wikipedia su History of silent reading per approfondire. ↩

5. Citazione originale in francese: Je n'ai fait celle-ci plus longue que parce que je n'ai pas eu le loisir de la faire plus courte. Consulta Quote Investigator per ulteriori informazioni. ↩

6. Ringraziamenti a Juraj Bednar per aver suggerito di usare il mistero di un omicidio come modo per spiegare il concetto di prova. ↩

7. La proprietà della sinteticità (succinctness) ha una definizione matematica precisa, ma non approfondiremo in questo articolo. Vedi ZKProof Community Reference per maggiori dettagli. ↩

8. I costi di transazione sono un concetto economico. Vedi la voce Wikipedia sui transaction costs. ↩

9. In un checksum, eseguiamo alcune operazioni basilari come addizioni e sottrazioni sulle cifre iniziali, e se il risultato finale non coincide sappiamo che qualcosa è andato storto. Curiosità: a differenza della maggior parte dei sistemi di identificazione, il Social Security Number (SSN) negli Stati Uniti non ha un checksum. Se un checksum è composto da una sola cifra, è chiamato check digit. ↩

10. Anche se più comune nei paesi meno sviluppati, ciò è successo recentemente anche con fallimenti bancari negli Stati Uniti. Vedi la voce Wikipedia sugli effetti del Collapse of Silicon Valley Bank. ↩

11. Citazione completa: "È un errore profondo, ripetuto da tutti i libri di testo e dalle persone eminenti nei loro discorsi, quello di coltivare l'abitudine di pensare a ciò che facciamo. È vero esattamente il contrario. La civiltà avanza aumentando il numero di operazioni importanti che possiamo eseguire senza pensarci. Le operazioni mentali sono come le cariche di cavalleria in una battaglia: sono rigorosamente limitate nel numero, richiedono cavalli "freschi" e vanno utilizzate solo nei momenti decisivi." Vedi Wikiquote. ↩

12. La calcolatrice di Pascal, la Pascalina, è una calcolatrice meccanica che suscitò grande ammirazione al suo lancio nel 1642. Vedi Pascal's calculator. ↩

13. Nei sistemi di autenticazione ben progettati, nemmeno il provider vede la tua password, ma soltanto un hash salato. Vedi Wikipedia sulla form of stored passwords. ↩

14. SHA256 è una funzione di hash crittografica molto utilizzata. Vedi SHA2. ↩

15. Puoi verificare personalmente questa operazione con un SHA256 calculator online o sul tuo computer tramite il comando sha256sum. ↩

16. La crittografia studia come proteggere le informazioni e nasconderle agli avversari. È una disciplina che combina matematica, informatica e ingegneria. Puoi approfondire la funzione e lo scopo degli hash crittografici qui. ↩

17. Tecnicamente, questa operazione si chiama dimostrare la conoscenza della pre-immagine di un hash. ↩

18. Vedi i Federalist Papers. ↩

19. Vedi questo articolo sulle group signatures scritto da 0xPARC. Include il codice Circom corrispondente. ↩

20. Le Zero Knowledge Proofs esistono dal 1985, e i loro autori hanno successivamente ricevuto il Premio Gödel per il loro lavoro. Possiamo fare un confronto con la crittografia a chiave pubblica, che impiegò decenni prima di essere utilizzata in tecnologie come il TLS, ora elemento fondamentale per un utilizzo di Internet sicuro. ↩

21. Ad esempio, il Lambda calcolo con i numeri di Church e il Lisp erano inizialmente teorici e poco pratici quando proposti. Dan Boneh e altri hanno fatto notare che rendere quasi-lineare il tempo del prover è ciò che ha reso pratiche le ZKPs, anche teoricamente. Vedi qui. ↩

22. Vedi le origini di Zcash nel paper Zerocoin. ↩

23. La resistenza alla censura significa che chiunque può effettuare transazioni su una blockchain pubblica senza permessi, a patto che rispetti le regole del protocollo. Significa anche che è molto costoso per un attaccante alterare o interrompere il funzionamento del sistema. La trasparenza indica che le transazioni sono pubblicamente verificabili e immutabili sulla blockchain per sempre. Questi concetti sono strettamente legati alla decentralizzazione e alla sicurezza, e rappresentano gran parte del valore delle blockchain pubbliche rispetto ad altri sistemi. ↩

24. Le firme BLS utilizzate nell'Ethereum Consensus Layer sono state implementate per proteggere miliardi di dollari pochi anni dopo il loro sviluppo. Vedi Wikipedia per approfondimenti sulle BLS Signatures. ↩

25. Dan Boneh, professore di crittografia applicata a Stanford, è un ottimo esempio di questo, vista la sua partecipazione a numerosi progetti legati alle criptovalute. ↩

26. L’autore ne ha sentito parlare da gubsheep di 0xPARC, ma il concetto è emerso più volte. Questo rispecchia anche l’esperienza personale dell'autore, che lavorando su RLN ha notato miglioramenti di uno o due ordini di grandezza nel tempo di generazione delle prove in pochi anni. ↩

27. In ambito giuridico, i falsi positivi possono capitare: vedi ad esempio l’Innocence Project. Tuttavia, in ambito matematico possiamo definire con precisione la probabilità di questi falsi positivi, rendendo il gioco decisamente impari. È il potere della matematica. Approfondiremo questo aspetto nei prossimi articoli dedicati alle prove probabilistiche. ↩

28. Probabilmente vorresti porre qualche domanda aggiuntiva a Sherlock Holmes prima di gettare il sospettato in prigione. Potrebbe infatti essere che Sherlock Holmes stia tentando di ingannarti! Nelle ZKP si assume sempre che il dimostratore (prover) non sia fidato. ↩

29. Questo risultato si ottiene utilizzando l’euristica di Fiat-Shamir. ↩

30. A volte si fa una distinzione tecnica tra i due concetti (solidità computazionale vs statistica), ma non è qualcosa di cui dobbiamo occuparci adesso. Vedi ZKProof Community Reference per approfondire. ↩

31. Alice e Bob sono personaggi comunemente utilizzati nei sistemi crittografici. Vedi Wikipedia. ↩

32. Esistono anche gli zk-STARK, quindi un nome più accurato potrebbe essere (zk)S(T|N)ARKs. Ovviamente è un po' complicato da pronunciare, quindi si preferisce semplicemente la sigla ZK. Ad esempio, vedi il nome del podcast ZK, lo standard ZK proof, ecc. Secondo l’autore, la Zero Knowledge è la proprietà più "magica" delle ZKP. ↩

33. Le fasi iniziali (setup) sono complesse e rappresentano una parte importante delle ipotesi di sicurezza nelle ZKP. Richiedono nozioni matematiche avanzate e meriterebbero un articolo dedicato per essere approfondite adeguatamente. Esiste un ottimo podcast divulgativo sulla cerimonia svolta da Zcash nel 2016 che puoi ascoltare qui. ↩

34. Tecnicamente, si tratta di un circuito aritmetico (arithmetic circuit) che gestisce operazioni numeriche, ma non introdurremo dettagli in questo articolo. Per approfondimenti vedi ZKProof Community Reference. ↩

35. A meno che tu non lo voglia! Le ZK sono a volte chiamate "Magic Moon Math" (matematica lunare magica), ma se studi veramente l'argomento, la matematica necessaria per intuire il funzionamento non è così complessa come si potrebbe pensare. Non approfondiremo in questo articolo, ma puoi vedere una presentazione dell’autore sulle basi matematiche delle ZKPs. ↩

36. Dal francese: eccoti servito, voilà, ta-da, ed ecco fatto. ↩

37. Esistono diverse definizioni di "succinctness" (sinteticità), e dipendono dal sistema di prova specifico. Tecnicamente, chiamiamo succinta una prova se la sua complessità temporale è sublineare. ↩

38. Attribuita a William Gibson, vedi qui. ↩

39. Con diverse nuove versioni in sviluppo, come Aztec e Railgun. Tornado Cash (archivio) funziona in modo molto diverso da Zcash, agendo principalmente come un mixer. Tornado Cash è stato recentemente sanzionato dal governo statunitense. Nel momento in cui scriviamo ci sono ancora molte incertezze sul caso, ma è stato un evento controverso che ha portato a diverse cause legali. Alcuni lo vedono come il seguito delle Crypto Wars degli anni '90. Ci sono altre alternative come Monero e Wasabi Wallet, che non si basano su ZKP ma perseguono obiettivi simili. Puoi approfondire leggendo Case for Electronic Cash del Coin Center. ↩

40. Vedi Semaphore del Privacy & Scaling Explorations team. ↩

41. Questo approccio è simile al funzionamento del sistema bancario tradizionale, in cui esistono molteplici livelli di regolamento nascosti all'utente finale. Vedi L2Beat per una panoramica delle diverse soluzioni Layer 2, incluse le ZK Rollups. Consulta anche Loopring, dYdX e Starknet. ↩

42. Esistono diversi tipi di zkEVM, con differenze anche piuttosto sottili. Vedi questo articolo di Vitalik per ulteriori dettagli. Consulta anche Polygon zkEVM, zkSync Era. ↩

43. Piattaforme o funzioni "SNARK-unfriendly" si riferiscono al fatto che la maggior parte delle primitive informatiche moderne sono state progettate per architetture specifiche, molto diverse da ciò che risulta naturale quando si scrivono vincoli per circuiti. Ad esempio, la funzione hash SHA256 è tipicamente considerata SNARK-unfriendly. Per ovviare a questo problema, alcuni progettano funzioni SNARK o ZK-friendly come la funzione hash Poseidon, pensata specificatamente per essere usata nelle ZKPs. Queste funzioni sono più facili da implementare nei circuiti ZKPs e possono essere 100 volte o più efficienti, anche se introducono altri compromessi. ↩

44. Mina permette una verifica succinta di tutta la blockchain, mentre Aleo si concentra di più sulla privacy. Vedi anche Mina e Aleo. ↩

45. In Dark Forest, alcune persone scrivono bot molto complessi che giocano autonomamente. Alcuni gruppi formano persino DAO private e creano smart contract che giocano semi-autonomamente. ↩

46. Telepathy di Succinct Labs è un esempio di questo tipo di progetto. Anche zkBridge ne è un altro, e probabilmente ne esistono molti altri ancora. ↩

47. Un'affermazione insolita, ma sorprendentemente accurata. ↩

48. Proof Carrying Data di 0xPARC è uno di questi esempi. Vedi PCD. Vedi anche Sismo. ↩

49. Non approfondiremo qui questi progetti, ma invito i lettori curiosi a cercare online per scoprire come diversi progetti utilizzano o stanno pensando di utilizzare le ZKP per raggiungere i propri obiettivi. Alcuni esempi: Unirep, Interep, RLN, RLNP2P, MACI, Filecoin, Stealthdrop, ETHDos e molti altri. ↩

50. Vedi ⁴² sopra per maggiori informazioni su questa distinzione. ↩

51. LLVM e WASM sono tecnologie relative a compilatori e toolchain. In estrema sintesi, consentono di scrivere codice in linguaggi di programmazione diversi che possono essere eseguiti in ambienti differenti, come vari browser web o tipologie diverse di computer. Comprendere i dettagli di questi sistemi non è rilevante ai nostri fini; ciò che conta è che ci permettono di scrivere ed eseguire programmi in ambienti molto eterogenei. Vedi LLVM e WASM. ↩

52. Vedi Delphinus Labs, RISC Zero, Orochi Network e nil.foundation. ↩

53. Vedi zk-MNIST ed EZKL. Ci sono anche progetti dedicati a reti neurali utilizzando sistemi di prova più moderni ed efficienti come Nova. ↩

54. Vedi l’articolo sull’uso delle ZK per combattere la disinformazione. ↩

55. Vedi questo saggio di ludens su 0xPARC per ulteriori dettagli su quest’idea. ↩

56. Vedi TLS Notary. ↩

57. Vedi questo articolo (archivio). ↩

58. A differenza delle Zero Knowledge Proofs, che consentono di dimostrare affermazioni su dati privati, la Multi-Party Computation (MPC) generalizza questo concetto permettendo calcoli su segreti condivisi. Ad esempio, se Alice e Bob hanno ciascuno un segreto, si può scrivere un programma che combina questi segreti senza rivelarli. È ciò che si vuole in un contesto negoziale, dove è necessario confrontare informazioni private per raggiungere un compromesso accettabile. La maggior parte degli MPC esistenti oggi è piuttosto limitata e inefficiente, ma si tratta di un ambito di ricerca entusiasmante con grande potenziale. ↩

59. Una storia familiare: vedi Sears vs Amazon. ↩

60. Citazione tratta da un panel a Devcon5. ↩