零知識入門指南

本文由 Nicole、PinHao 和 Anton 翻譯

前言

零知識證明（Zero Knowledge Proofs, ZKPs）就像魔法，讓我們能實現過去連想都想不到的事。

先來幾段引言引發你的思考。有些你或許耳熟能詳，有些可能是你第一次聽到。

任何足夠先進的科技都與魔法無異。

• Arthur C. Clarke

文明的進步，來自於我們能「不假思索」完成的操作愈來愈多。

• Alfred North Whitehead

「我之所以把信寫得比平常還要長，只是因為我沒時間把它寫得更短。」

• Blaise Pascal

「隱私是你可以自由選擇要向世界揭露什麼的權力。」

• 《Cypherpunk 宣言》

未來已經到來，只是還沒有同比例地影響每個人。

• William Gibson

魔法般的科技、推動文明的力量、精煉的文字、隱私，以及已經抵達的未來——這些合起來就是零知識證明（ZKPs）的精髓。這是什麼意思呢？

在過去一百年間，電腦與網際網路席捲全球，滲透我們的所有行為，這帶來了好處也帶來麻煩。在這之上誕生了各種平台、公司與帝國，例如 MAMAA（Microsoft、Apple、Meta、Alphabet、Amazon）等巨頭；再往下是巨獸的腹部——支付網路、政府服務，以及那些無聲無息卻撐起世界運轉的大量 B2B 應用；最後還有長尾應用們：可愛的濾鏡相機、語言學習平台、線上社群等等。

每當你把資料餵給某個線上服務時，總是期待可以達到什麼目的——或許只是聯絡朋友、轉移注意力，也有可能是像申請房貸這樣的大事。但這些資料最終會如何被處理？除了你已知的資訊，其實還有隱藏在冰山下的大量資料。事情真的會如你所想嗎？還是會在此時此刻或是一年後發生什麼問題？

究竟誰能真正理解這些系統，以及我們的使用方式會帶來什麼後果？它們又如何反過來影響我們？有人或許精通某些系統，但沒有人能通曉全部，更遑論它們交互作用後產生的意外效應。

那人類該怎麼辦？我們只能依賴「信任」。但該信任誰？又憑什麼？

這是一道艱難的課題。人腦並未進化到可以處理如此抽象的信任問題。網際網路雖然讓人們更緊密連結，但也讓局面更加複雜。在以前，私下的談話會隨著風吹而消逝；忘了帶鑰匙，你可以找鎖匠，或自己撬開門鎖。如今被鎖在 Google 帳號外，看著「拒絕存取」，你能找誰？就像站在無形且堅不可摧的城牆。

ZKP 或許無法立刻、全方面的解決所有問題，但在許多場景中，它的影響正與日俱增。接下來的內容，我將說明它「為什麼」重要，以及「如何」運作。讓我們追隨這股魔法吧！

什麼是零知識證明？

本節將介紹「零知識證明」的基本概念

這篇文章是零知識證明系列的第一篇——我們將依序介紹它是什麼、為何值得關注、如何運作，以及可以應用在哪些領域。

想像你走進酒吧，你可以在不透露生日資訊的狀況下，證明自己已經年滿 18 歲。酒保只需知道「這個人是否達到合法飲酒年齡？」這一個特定的資訊，而 ZKP 恰好可以只揭露這一點。

ZKP 讓你僅揭示「敘述為真」這件事，而不洩漏其他任何資訊。

這代表什麼？讓我們用經典的「威利在哪裡？」範例說明：你想讓對方相信你知道威利的位置，卻不透露確切地點，該怎麼做？

假設我有一張「威利在哪裡」圖片，再拿一塊挖有小洞的厚紙板蓋上去，只讓威利透過小洞露出。你見到威利，自然相信我知道他的位置，但對整張圖的其他細節仍一無所知。

這顯然只是個玩具示例，但希望能讓你初窺 ZKP 的威力。我們稍後會更深入探討，先來概覽 ZKP 能帶來哪些益處。

透過 ZKP，你可以用通用方式證明任意敘述。相較於傳統數學證明往往冗長，ZKP 能在兼顧隱私的前提下，精簡地完成同樣任務。

接下來你會看到，這種能力有多麼強大。

為什麼你應該在乎？

本節將說明你為何應該關注 ZKP，從隱私、壓縮到其通用性

看完上節你可能會想：「好酷，但我已經有密碼和 TLS，這樣不就夠了？」事實並非如此。ZKP 開啟了截然不同的新能力。

隱私是「選擇性地向世界揭露自己」的能力。

• 《Cypherpunk 宣言》¹

對話、密碼、信用卡資料——這些資訊都需要基本的隱私。沒有隱私，線上購物或私人通訊就不可能實現。

你也許認為「我們已經能保護密碼不外洩」，但 ZKP 帶來的是「可程式化的隱私」。試想：在不透露身份的前提之下，證明自己是獨一無二的存在；或證明自己符合法規，卻不揭露商業機密——ZKP 皆可辦到。

你或許會想：「我們已經能把密碼之類的東西保密，有什麼好大驚小怪的？」在這些具體例子上，你說得沒錯。但若要真正理解「通用且可程式化的隱私」能帶來的潛力，就得發揮更大的想像力。

舉例來說，Augustine 在《懺悔錄》（公元 400 年）中記載，主教 St Ambrose 會「默讀」這件事，在當時相當少見。那個年代，人們通常是邊讀邊念出聲音。²

當 Ambrose 閱讀時，他雙眼掃過頁面，心中體悟意義，但口中無聲、舌尖不動。任何人都能自由走近，他也不常被告知有客人來訪，因此我們造訪時，常見他如此靜靜閱讀，從不朗讀。

現今默讀被視為理所當然，甚至難以想像它曾是一項發明。「閱讀內容只屬於閱讀者本人」的概念當時極為陌生。那麼在當代，還能出現哪些類似的新發明？也許是我們現階段難以想像的事物。

接下來我們將窺見利用 ZKP 的發明——無論既有或即將問世——會是什麼模樣。

Compression 壓縮

「我之所以把信寫得比平常長，只因為沒時間把它寫短。」

• 布萊茲．帕斯卡（Blaise Pascal）³

壓縮（compress）的定義是：

「將某物壓入更小的空間」

同樣地，精簡性（succinctness）被定義為：

用極少字句來清楚表達

ZKP 具備壓縮特性，代表我們可用極短的敘述來證明某件事為真，例如一段運算的所有步驟皆正確執行。當某項資源供不應求且成本高昂時，這格外實用；Ethereum 區塊鏈就是其中之一，當然也在其他場合同樣受益。更厲害的是，無論你想證明的內容有多複雜，證明（proof）的大小幾乎不變！

何謂「證明」以及「證明大小」？在數學裡，這些概念精確且細膩。我們稍後會深入 ZKP 背景下的「證明」概念；目前可將其視為一段我們確信、或能驗證其為真的短敘述。

在經典的福爾摩斯式推理中，偵探會蒐集證據，直到能證實犯人確實行兇，並在最終解謎時詳述自己如何得知。這段最終陳述即可視為證明。⁴

更正式地說，此特性稱為 精簡性（succinctness）。⁵ 正因如此，證明大小與要證明的內容複雜度無關。在公鏈的情境下，這也與 可擴展性（scalability） 相關。對於 Ethereum 這類區塊空間有限且昂貴的公鏈，ZKP 能讓交易更便宜、更快速：我們只將「某批交易已完成」的精簡證明上鏈，而不是把所有交易數據寫入鏈上，同時仍保有高度安全性。

精簡性本就與區塊鏈無關，只是各種因素讓二者十分契合。更普遍地說，若能用短小證明保證某事為真，就非常實用；原因可從數個角度理解。

其中一種考量是 交易成本。⁶ 一般而言，成本越低，就能創造更多價值與財富；若需驗證的事項更少或更簡單，行動自然更自由、輕鬆。

有時填寫表單會要求我們重複輸入電子郵件，以避免手誤；又如包裹單號、信用卡號或 ISBN 內多出一位檢查碼，藉此簡易驗證數字是否正確。顯而易見，這些機制並非防範惡意行為，而是杜絕無心疏失。⁷

在電腦檔案系統中，常使用雜湊函數（hash） 來驗證檔案完整性。即便檔案僅有一小部分受損，其雜湊值也會完全改變。由於雜湊值十分精簡（例如僅 64 個字元），即使檔案本身很大，也能輕鬆保存並比對。透過雜湊函數可安全地確保完整性；比起備份整個檔案更加高效。無論檔案大小如何，雜湊值長度始終一致；正是這種精簡特性，造就了上述應用。

你知道嗎？

讓我們暫時撇開壓縮、精簡性與證明，先討論「知識」、「心理負擔」與「信任」，並在本節末尾再將它們與 ZKP 串連起來。

日常生活中，你如何判定某件事為真？若你每天都看見日出，自然相信明天也會再看見。在現代社會中，我們很大程度上受到了保護，免於面對自然界嚴酷的環境，但另一方面，我們卻有許多其他更現代的煩惱。這些煩惱有許多都與我們日常打交道的各種機構有關。

如果你每天都能從銀行提領現金，你會預期隔天仍能順利提領嗎？大多數人會說「會」，但並非永遠如此。這取決於多項因素：銀行是否可信、所處區域是否安全、近期全球經濟是否有突發大事、你的個人情況等等。統整這些資訊後，你才會做出判斷。

這當然只是簡單的例子，但生活中充斥著類似的互動。這些判斷會造成一種心理負擔；負擔的嚴重程度，取決於個人處境及日常事務的複雜度。例如企業在簽訂合約時，往往得更謹慎評估上述因素。

我們建立了各種機制與規則來應對這種不確定性，例如：使用信譽評級服務、進行獨立審計、實施罰款以遏止不良行為、尋求權威機構的認證。 這些措施本質上都是權宜之計，試圖觸及問題的核心：事物是否如其所聲稱的那樣？是否符合我們制定的規範？是否值得信賴且具實用性？

當你同時面對多個機構、公司與對象時，心理負擔會層層疊加，並可能引發連鎖效應：例如銀行倒閉導致你無法支付員工薪資，進而令業務無法服務客戶⁸。這時需要更多控管手段，我們不得不更常停下來檢視「事情是否正常、可能出什麼差錯」。

我以一段引言結束本節：

文明的進步，來自於我們能「不假思索」完成的操作愈來愈多。

• Alfred North Whitehead ⁹

舉例來說，煮飯時，你不用思考如何生火；這與過去撿木柴、晾乾、引燃並持續維持火勢的繁瑣流程截然不同。在數學領域，若無微積分，我們也無法登月。

透過 ZKP 與精簡證明，我們能為本質不透明的系統注入更高確定性與清晰度。當我們考慮 組合（compose） ZKP ——例如透過聚合（aggregation）或遞迴（recursion）將多份證明合為一體——其威力更是倍增。

要達成此目標，前提是能將上述往往雜亂、不一致的機制或規則，轉化為 ZKP 可理解的形式。我們該如何辦到？

通用性

回想一下，ZKP 能以通用方式證明任意敘述。這為何重要，又有何威力？

類似工具與 ZKP 的差異，就像計算機與電腦的差別：前者為特定任務而生，後者則為通用。這就像下圖的古早計算機¹⁰與現代電腦之別：

前文提及的密碼與雜湊值，更具體說明了隱私與精簡性的應用：密碼是一段私密資訊，使你得以登入服務¹¹；對於檔案等輸入資料而言，其雜湊值提供了一種精簡方式來驗證相等性。

我們可以用下圖呈現雜湊函數：

我們對已知的輸入資料套用特定的雜湊函式（例如 SHA-256¹²）。以英文句子「The quick brown fox jumps over the lazy dog」（不含引號）為例，經過 SHA-256 雜湊運算後會得到雜湊值d7a8fbb307d7809469ca9abcb0082e4f8d5651e46d3cdb762d02d0bf37c9e592。若在句尾加上一個「.」，則會產生完全不同的雜湊值：「The quick brown fox jumps over the lazy dog.」的雜湊結果是ef537f25c895bfa782526529a9b63d97aa631564d5d789c2b765448c8635fb6c。

即使句子只有小小地改動，最終雜湊值也截然不同¹³。 安全的雜湊函數難以被「破解」，且具備幾項重要特性。例如：即使知道雜湊值，也無法逆向還原原始輸入資料；同時，要刻意構造出能產生特定雜湊值的訊息也極為困難。這類具備加密強度的雜湊函數，我們稱之為「密碼學雜湊函數」¹⁴。

上述 SHA256 屬於特定密碼學雜湊函數，經過大量時間與專家們確保安全性。僅靠雜湊值本身無法證明任何事，唯有在與原始訊息或檔案等參照物進行比對時，這些雜湊值才具有實質意義。

簡單來說，我們可以將雜湊函式視為一種「特定訊息對應特定雜湊值」的證明機制。但關鍵在於，唯有持有原始訊息才能進行驗證。有人會利用這特性來證明原創性與預測能力——例如先在推特公開發布一段預言訊息的雜湊值，內容可能是：「2040年4月1日，外星人將降臨倫敦大笨鐘頂端，且彩票號碼25742069將贏得頭獎」。當預言成真時，他們再公開原始訊息，這時眾人通過雜湊值比對，就會相信他們確實預知未來。

我們可以用下圖呈現 ZKP：

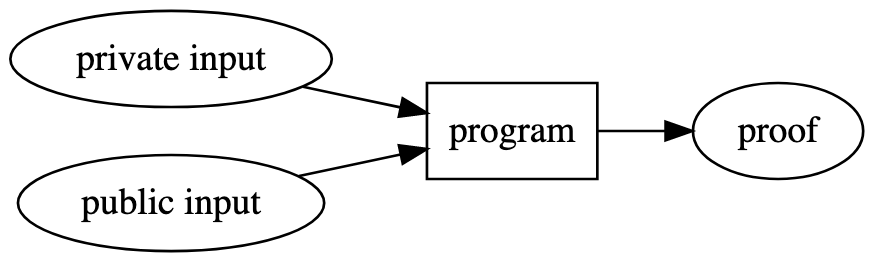
與上述雜湊函數示意圖相比，這裡有幾個重大差異：

• 相較於只有單一（公開）輸入的架構，我們採用了同時包含多重私有輸入與公開輸入的設計模式
• 可使用任意程式，而非侷限於密碼學雜湊函數
• 我們產生了一個可獨立驗證的完整證明

在上述雜湊函數的範例中，我們必須公開輸入值才能驗證訊息與雜湊值的對應關係。而在零知識證明（ZKP）中，我們還可以引入「私有輸入」——這些是只有你自己能看到的資料。也就是說，你無需向任何人揭露這些私有資料，就能產生有效的證明。

例如，回到本文開頭的「威利在哪裡」案例，公開輸入就是那張尋找威利的圖片，私有輸入則是威利的實際位置。我可以產生一份證明，讓你相信我知道威利在哪裡，但不揭露那個私有輸入——威利的位置。

同理，若我手上有一題數獨（流行的邏輯謎題），我也能證明自己知道解答，卻不揭露答案。本例中，公開輸入是初始題盤，私有輸入則是完整解答。

你可能注意到，尋找威利與解數獨是截然不同的問題。然而，我們可以編寫一個簡單程式，既能表達這兩種問題的運作原理，又能運用零知識證明（ZKP）來產生證明。這是因為此特殊程式內部的邏輯具有通用性，能夠執行任何電腦可完成的運算。

如此一來，我們把原本屬於密碼學或數學領域——設計並強化某個密碼學雜湊函數——的問題，轉化為程式設計問題。以下幾個例子能展現這種轉變的威力。

如今，我們可證明自己持有能對應到特定雜湊值的私有資料¹⁵。換句話說，你可以證明自己擁有某份訊息（例如重要文件），但不必公開其內容。

為進一步理解通用運算的力量，讓我們仔細檢視群簽章（group signature）。群簽章允許多人共同為文件簽名，卻不透露各自身份。例如《聯邦論》作者們共同使用「Publius」這個筆名來簽署文章¹⁶。與 SHA256 雜湊函式類似，我們能透過密碼學與數學方法來實現群簽章，這項技術的開發需要極其複雜的密碼工程。但藉由通用型零知識證明（ZKPs），任何人只需用 ZKP 專用程式語言 Circom 編寫幾十行程式碼¹⁷，就能實現相同功能。

由於其通用特性，我們可以輕鬆打造某種情境之下的專屬解方。例如，你的身分證上印有姓名、住址等個資；若要進場活動，你須證明年滿 18 歲並持有有效票券，但又不想讓陌生人或線上系統看到住址，或冒著身分證被盜的風險。利用 ZKP，你可以證明：

• 你持有有效身分證
• 此證件在過去五年內由合格的機關簽發
• 該證件近期未被註銷或報失
• 你已滿 18 歲
• 你已購買有效入場券
• 該票券從未被使用

除了上述列舉的資訊外，關於你的其他資訊都不必公開。

有了 ZKP，我們手中多了一把「更好用的工具」，能在各種場景中協調互動，尤其適用於對「隱私」 與「精簡性」有高度需求的系統。更多應用案例將於後續章節呈現。

往往是想像力限制了你的超能力

為什麼是現在？

為何零知識證明（ZKP）近年來大放異彩？其中既有技術因素，也有社會因素。

就技術層面而言，ZKP 屬於相當新的概念。從數學上看，它們僅問世數十年¹⁸；如同電腦本身，從理論到真正足以實用與高效，也花了不短時間¹⁹。

之後，必須有人將這些理論論文與密碼學協議轉化為實際應用。2016 年推出的隱私加密貨幣 Zcash 是首個重要案例，其最初只是密碼龐克（cypherpunks）與研究人員撰寫的學術論文²⁰。初版 Zcash 把研究與工程成果落地為一套完整系統，雖然存在許多缺陷且遠遠不到完善，但它是 ZKP 首度在真實世界大規模應用的實際例子，向世人證明 ZKP 的可行與實用性，也因此引爆近年 ZKP 的研究與開發浪潮。

像 Ethereum 這類公鏈與強調隱私的 Zcash，在推動 ZKP 上扮演了關鍵角色。區塊鏈天生擅長抗審查與透明度²¹，卻犧牲了隱私與擴充性，而 ZKP 正好補足這兩點。再加上鏈圈對先進密碼學的高度興趣²²，創新自然在區塊鏈與 ZKP 的交界處不斷湧現²³。大量資金充裕的區塊鏈專案，也把傳統偏學術的 ZKP 領域帶進更多研發投資。

ZKP 橫跨應用數學、密碼學、各種特定系統論文、新型證明系統實作、開發工具及多元領域應用，複雜度極高，但發展速度更是驚人；幾乎每年、甚至每月都出現新研究、新工具與新應用。研究成果、實作與落地的迴路愈發緊密。雖然仍具挑戰，但入門門檻正隨工具完善而大幅降低，開發者對底層數學的理解需求也漸減。

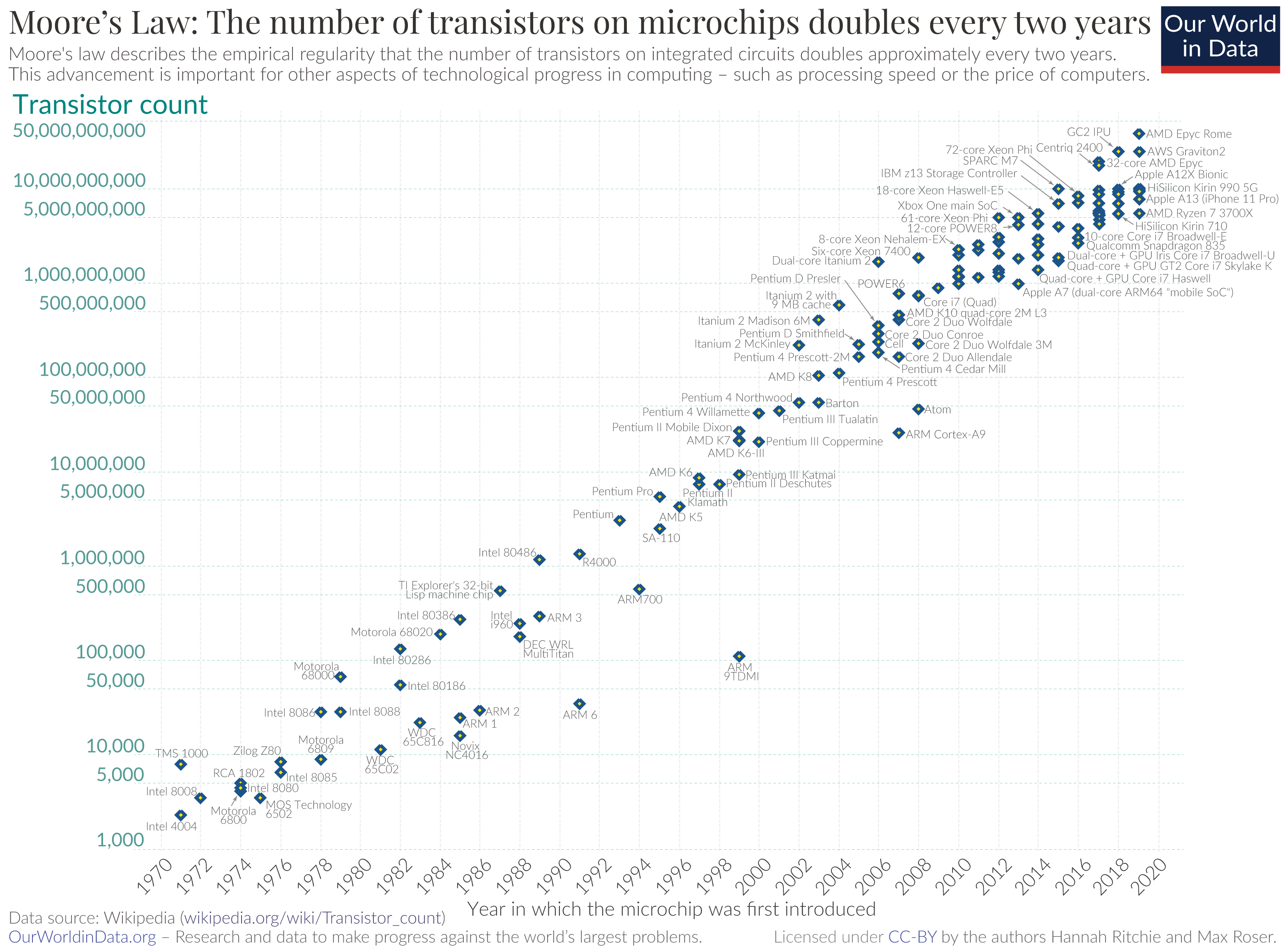
就效能而言，ZKP 似乎也呈現類似摩爾定律的增長。摩爾定律指晶體管數量約每兩年翻倍，推動了電腦革命；在 ZKP 領域，幾年前仍被視為遙不可及的 zkVM、zkML 如今已進入實作階段。經驗顯示，ZKP 方案大約每隔兩年就能提高一個數量級²⁴。由於這項技術仍新穎，從程式、系統到硬體，各層可積極最佳化，暫看不到增速趨緩的跡象。

運作原理概覽

本節將概括性地介紹 ZKP 的運作方式，無需數學公式或程式碼。

基礎概念

首先讓我們建立一些基本術語。雖然需要學習幾個新名詞，但隨著說明你會逐漸熟悉他們。

• 協議（protocol）：一套規則，說明各方應遵循的正確行為
• 證明（proof）：用來確立某敘述為真的論證
• 證明者（prover）：提出或展示證明的一方
• 驗證者（verifier）：確認證明正確性的一方
• 私有輸入（witness）：僅證明者可見的輸入
• 公開輸入（instance）：證明者與驗證者皆可見的輸入

了解術語很有幫助，但恰當的比喻能讓人更快抓住核心概念；後續我們還會引入更多關鍵術語。

協議無所不在，他可能是隱含的也可能是明確的。以西洋棋為例，其協議是兩名玩家依規則輪流下棋，直到決勝負或達成和局。理論上每一步所花費的時間不影響結果，但實務上我們會盡量減少雙方互動成本，可將其想像成「超高速下棋」。

我們也可將福爾摩斯視作證明者，他在最終案情的陳述中，構築了一系列精妙的論證（即證明），指認某人為兇手。此證明需由驗證者——如法官或陪審團，並達到「排除合理懷疑」的司法標準²⁵。 由於該證明本身具有==自主性==，任何人都可以擔任驗證者角色，包括正在閱讀的你——唯有當你被提供的推理邏輯說服時，這個偵探故事才具有可信度²⁶。

私有輸入可想成只有福爾摩斯知曉的線索，例如他人私下告訴他的祕密。這在 ZKP 術語中稱為 witness，可能源自法庭上的「證人」握有私密資訊並用以作證。於 ZKP 中，證明者不會將該私有資訊透露給驗證者（這裡即法官與陪審團）。

ZKP 建立起「證明者」與「驗證者」之間的「協議規範」。若二者無須直接互動，即為「非互動式」協議；當證明者與驗證者無需直接互動或交流時（例如下棋或共舞的情境），該協議即具備「非互動性」——證明者只需產生一份獨立的證明，後續再由驗證者進行驗證。多數 ZKP 最初都屬於「互動式協議」（需要多次來回溝通），而後透過數學技巧轉化為非互動式²⁷。可將非互動想像成兩位棋手交談幾句便預知彼此所有走法，因而不必真正開局。

ZKP 類型眾多，我們常提到 zk-SNARK，全名 Zero Knowledge Succinct Non-Interactive ARguments of Knowledge。Zero Knowledge 與 Succinct 分別對應前文隱私與壓縮，Non-Interactive 即非互動；ARguments of Knowledge 基本上等同於證明²⁸。zk-SNARK 自身也分許多變體。

理解零知識證明（ZKP）的最佳心智模型，就是將其想像成一座動物園。園內有各式各樣的「動物」（指各類證明系統），我們可以用不同方式分類：這些動物有四條腿、那些身上有條紋、去年由 Bob 引進的品種²⁹等等。某些分類方式比其他更有實用價值。事實上，部分系統甚至根本不具備「零知識」特性！這類系統通常就簡稱為 SNARKs。儘管如此，整個技術社群仍習慣將這座充滿各異「動物」的園區統稱為 ZK（零知識證明），即使當中許多系統實際上並未運用真正的零知識特性³⁰。

協議流程

回到我們的協議架構，當中包含證明者（prover）與驗證者（verifier）兩個角色。證明者會運用「證明金鑰」（prover key）、私有輸入（private input）及公開輸入（public input）來生成證明；而驗證者則透過「驗證金鑰」（verification key）與公開輸入進行驗證，最終輸出「真」（true）或「偽」（false）的判斷結果。

在此我們引入了兩個新要素：「證明金鑰」（prover key）與「驗證金鑰」（verifier key）。這對金鑰正是證明者與驗證者施展「密碼魔法」的關鍵所在。你可以將它們想像成： 實體鑰匙 - 如同開啟特定場所並執行操作的通行證 魔法手杖 - 賦予持有者施展特殊能力的媒介

這些金鑰源自一項稱為「設定儀式」（setup）的特殊程序——即我們不會在本文詳述的初始準備階段³¹。

關鍵在於，私有輸入（private input）只由證明者自己掌握。那麼，證明者究竟要如何結合「證明金鑰」、私有輸入與公開輸入（public input），最終產生證明呢？

回想之前的 ZKP 示意圖：

此處有一段特殊程式（正式術語稱「電路 circuit」），編碼了使用者關心的邏輯，例如證明自己知道能對應特定雜湊值的資料。與一般程式不同，電路由多個「限制式」（constraint） 組成³²；我們要證明的是，私有與公開輸入共同滿足所有限制條件。

最終，驗證者會取得這份簡短的證明，將其與「驗證金鑰」、公開輸入（public input）以及包含所有限制條件的特殊程式結合，經過嚴謹驗證後，在「排除合理懷疑」的標準下確保證明的正確性，並輸出 true；若驗證未通過，則輸出 false。

這樣的描述雖然經過一定程度的簡化，但確實掌握了整個機制運作的核心精髓。

限制式

那麼，構成上述特殊程式的「限制式」是什麼？例如「數字須介於 1 到 9」就是一條限制式，7 滿足，11 不滿足。如何把程式寫成一組限制式本身是一門藝術，我們先從簡單的數獨例子談起。

在數獨（Sudoku）這個遊戲中，目標是找出一組解，使整個棋盤符合一系列的限制條件。每一列都要包含 1 到 9 的數字，且只能出現一次。每一欄與每個 3x3 的子方格也都一樣。我們會被給定一個初始的棋盤，然後我們的任務是將剩下的空格填滿，並且讓所有限制都被同時滿足。困難的地方就在於要同時滿足這麼多限制條件。

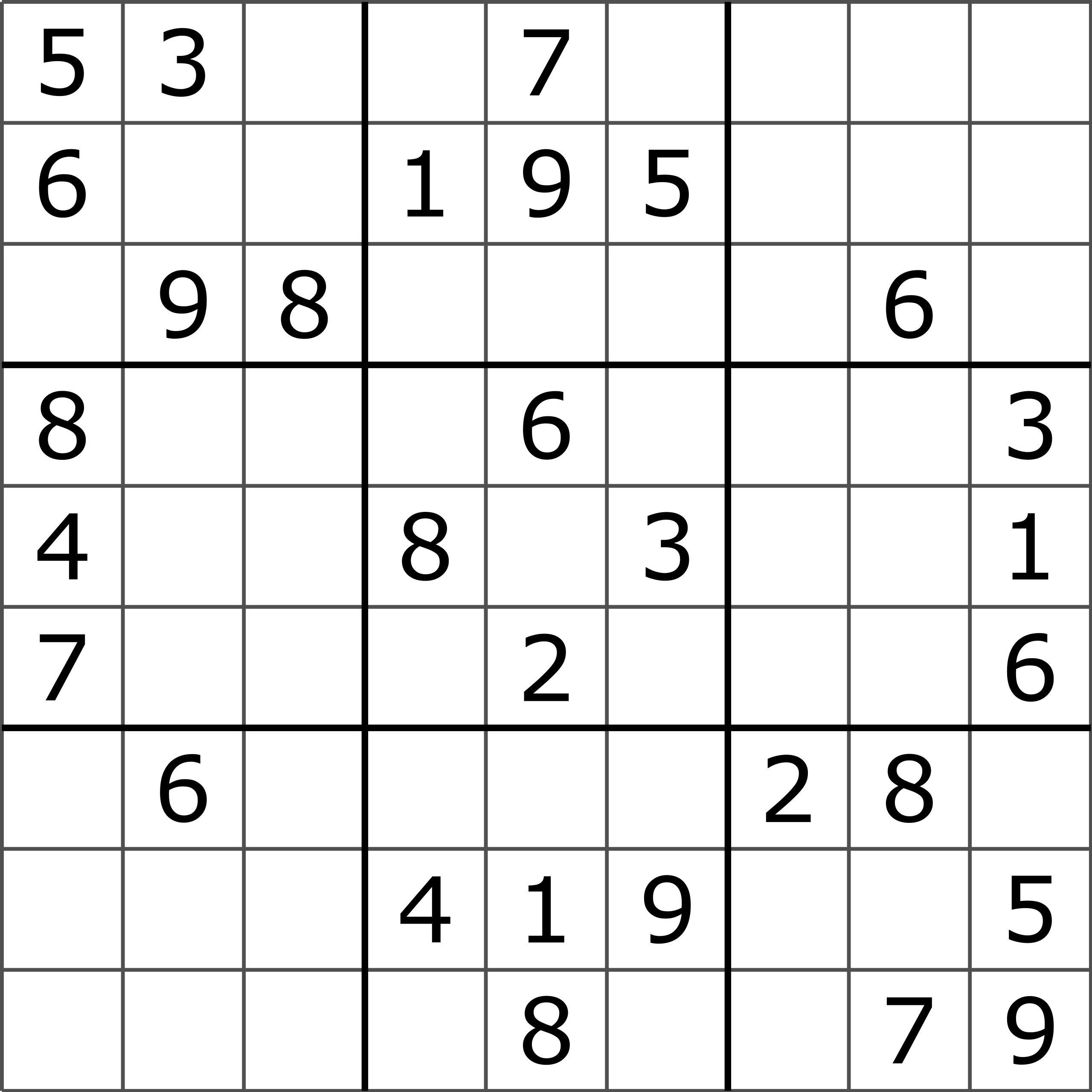
透過 ZKP（Zero-Knowledge Proof，零知識證明），證明者（prover）可以建立一個證明（proof），來證明自己知道某個謎題的解。在這個例子中，證明的過程會使用一部分公開輸入，也就是初始棋盤，以及一部分私有輸入，也就是他手上的解答，再搭配一個電路（circuit）。這個電路描述了構成這個謎題的所有限制條件。

我們稱它為電路（circuit），是因為這些限制條件彼此之間是相互連接的，就像電路中的導線一樣。不過這裡的電路不是傳導電流，而是傳遞數值。例如，我們不能把「banana」這種值塞進一個列的限制條件中，它必須是一個數字，且這個數字必須介於 1 到 9 之間，依此類推。

驗證者（verifier）擁有同樣的電路與公開輸入，並可以用來驗證證明者送來的證明。只要這份證明是有效的，驗證者就能確信證明者真的知道這個特定謎題的解。

事實證明，很多問題都可以被表達成一組限制式。事實上，只要是電腦能解的問題，都能被轉換成一組限制式。

數獨例子

讓我們把前面學到的 ZKP 組成部分，應用到這個數獨的例子上。

對於數獨來說，我們的特殊程式——也就是電路——會接收兩個輸入：

• 數獨題目作為公開輸入
• 數獨解答作為私有輸入

這個電路由一組限制式組成，而這些條件都必須被滿足。這些條件大致如下：

• 題目與解答中的所有數字必須介於 1 到 9
• 解答中已經填入的格子，必須與題目中原本的數字一致
• 每一列必須恰好包含一次數字 1 到 9
• 每一行必須恰好包含一次數字 1 到 9
• 每個子方格也必須恰好包含一次數字 1 到 9

如果這些限制條件對題目與解答都成立，那我們就知道這是一組正確的解。

證明者 Peggy 使用她神奇的證明者金鑰（prover key），搭配謎題與解答，與這個特殊的程式結合後產生一份證明。這份證明非常短，少於一千個字元。它包含了完成任務所需的所有資源（self-contained）的，也就是說驗證者拿到這份證明後就擁有了驗證所需的一切資訊。你可以把它想像成一個魔法咒語，它會幫你完成任務，而你不需要理解它背後的所有細節 ³³。

以下是由 Circom/snarkjs 套件所產生的一個零知識證明（ZKP）範例：

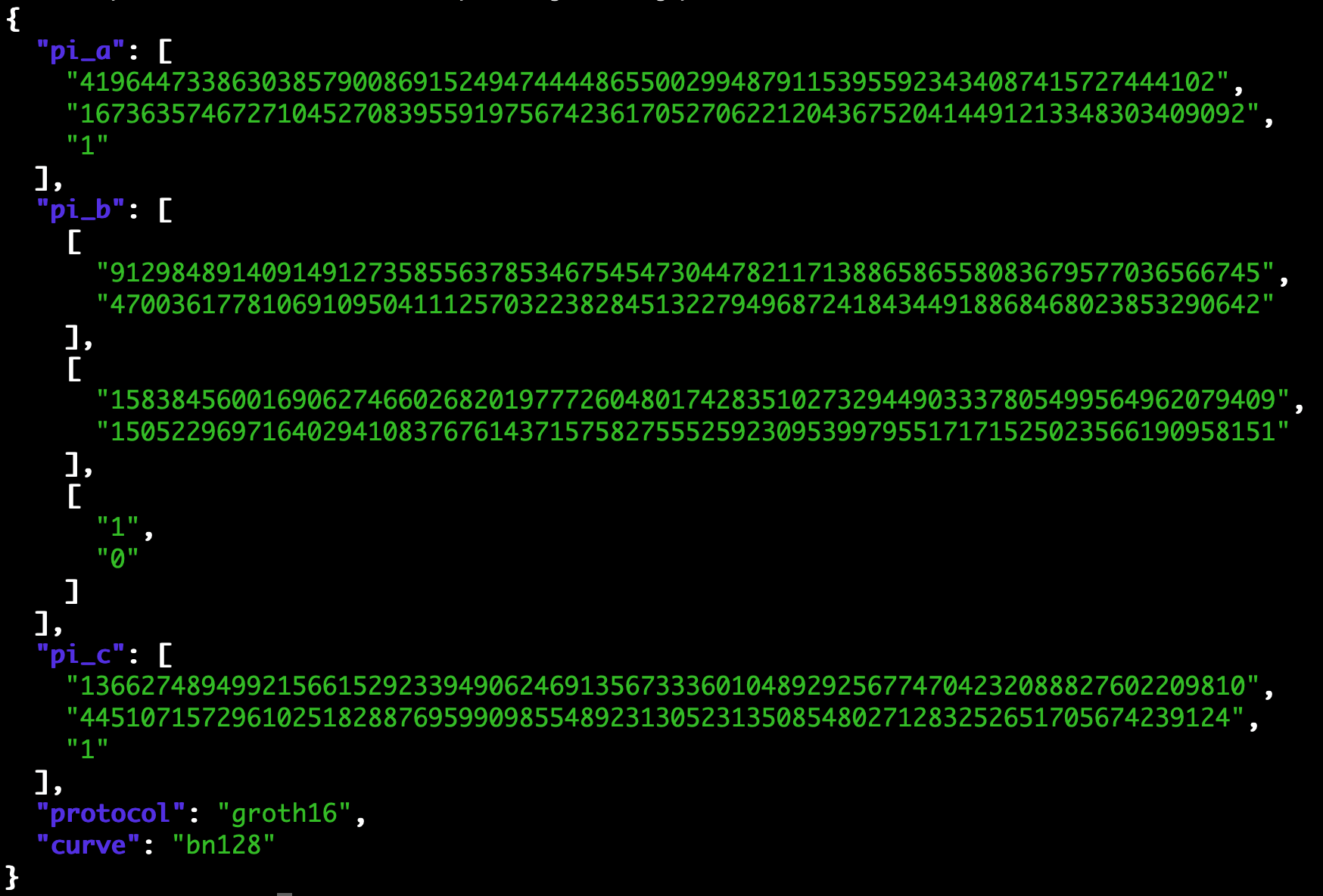
而在這個例子裡，這份「魔法」是真的有效的。

驗證者 Victor 使用他的驗證者金鑰（verifier key）與原始謎題輸入，來驗證 Peggy 所提供的證明是否正確。如果正確，輸出會是 "true"；如果不正確，輸出會是 "false"。這個魔法咒語要嘛成功，要嘛無效。就這樣，Victor 可以確信 Peggy 確實知道這個謎題的解答，而不需要實際看到解答本身。Et voilà！³⁴

幾個重要性質

ZKP（零知識證明）具備幾個技術上的重要性質：

• 完整性（completeness）：如果陳述是正確的，驗證者就會被證明說服
• 正確性（soundness）：如果陳述是錯的，驗證者幾乎不可能被說服，除了極小的機率
• 零知識性（zero knowledge）：如果陳述是正確的，證明過程不會洩漏除了「這件事是真的」之外的任何資訊

另外，對於 zk-SNARK 而言，證明具有精簡性（succinctness），也就是說即使程式變得複雜，證明的大小基本上不會變大 ³⁵。

在實際應用中，我們還會關心許多其他 ZKP 的性質：

• 這個系統是基於哪些數學假設？
• 它的安全性有多高？
• 是否需要信任設定（trusted setup）？
• 產生證明的難度如何？需要多少時間與資源？
• 驗證這份證明的難度與成本高不高？
• ZKP 系統是否支援將多份證明合併？
• 是否有適合開發者使用的 ZKP 程式庫？
• 用於撰寫這類 ZKP 程式的語言表達力如何？
• 以及其他種種

你可以看到，ZKP 的應用與設計有非常多種考量與變化。但不用擔心，核心概念基本一致。根據你的興趣所在，其實你可以不用理解所有技術細節也沒關係。回到動物園的比喻：你不一定要當生物學家，也許你只是想接觸幾隻動物、養個寵物，或甚至只是偶爾摸摸朋友的狗狗。

應用場景

本節會介紹目前已經出現與未來有潛力的 ZK 應用

ZKP 的應用非常多樣。整體來說，目前仍處於早期階段，主要聚焦在底層協議、基礎建設與區塊鏈相關的應用。若對區塊鏈已有一定理解，會更容易看懂這些例子，但並非必要條件。本節會介紹一些有趣的應用場景，先從目前已上線的應用開始，接著看未來可能出現的方向。

未來已經來臨，只是尚未平均分布。

• William Gibson ³⁶

已上線的應用

電子現金：若要在線上建立如同實體現金的支付系統，就必須具備「可替代性」與「隱私性」。可替代性（fungibility）指的是每個單位的資產沒有區別，你的錢與我的錢本質上沒有差別，都是可接受的支付方式。透過 ZK 技術，我們可以讓交易圖（transaction graph）保密，避免像比特幣或以太坊那樣的公開記錄。這讓電子現金保持可替代性。目前已實作於 Zcash 與 Tornado Cash 等系統中 ³⁷。

匿名訊號傳遞：有時我們需要證明自己屬於某個具備特定屬性的群體，但又不希望暴露身份。例如，證明你屬於某個團體，或是參與投票。這樣你就不需要將身份與敏感行為綁定，如投給哪個政黨，或洩漏其他不必要的資訊。這類機制已在 Semaphore 等系統上線，並有許多相關的變化 ³⁸。

ZK Rollup：讓交易速度更快、成本更低。目前以太坊主鏈（L1）的空間寶貴且交易需求龐大，因此出現了稱為 Layer 2（L2）的擴容方案。L2 在主鏈外處理交易，當累積到一定數量後再打包回 L1。ZKP 非常適合這個流程，因為它能（1）證明交易執行正確，（2）生成精簡的證明佔用主鏈空間極小。如此一來用戶能以幾乎相同的安全性享有更便宜快速的交易體驗。由於要證明整個以太坊虛擬機（EVM）執行過程十分困難，因此目前的 ZK Rollup 多專注於簡單資產的交換。已上線系統包括 Loopring、zkSync Lite、dYdX 與 Starknet ³⁹。

ZK-EVM：和 ZK Rollup 類似，但具備通用性，能處理任何類型的交易與程式。以太坊的 EVM 本質上是一台全球共用的通用型電腦，任何人都能在上面執行程式。我們可以用 ZKP 對這些程式的正確執行過程建立證明，並生成精簡的結果，確認執行無誤。這有多種用途，最直接的是擴容與降低交易成本。目前已上線的系統有 Polygon zkEVM、zkSync Era，許多其他專案也正在開發中 ⁴⁰。

ZK-VM：由於以太坊的 EVM 本身不太適合 ZK 證明（被稱為 "snark-unfriendly"），許多項目選擇重建一條與以太坊無關的新鏈，並設計出對 ZK 更友善的虛擬機（VM）。根據具體系統設計，這些平台能更有效率地驗證區塊鏈狀態並保護隱私。目前 Mina 已上線，Aleo 等系統仍在積極開發中 ⁴¹。

Dark Forest：Dark Forest 是一款僅提供給玩家部分資訊的即時戰略遊戲。基於 ZK 的遊戲能實作所謂「加密迷霧」，玩家僅能看到一部分遊戲世界，這種視野限制是由 ZKP 保證的。與 Starcraft 等傳統遊戲不同，甚至連伺服器本身也無法看到所有資訊。這種可程式化的特性開創了全新的遊戲體驗方式 ⁴²。

ZK 橋接（Bridges）：橋接協議可讓你在不同區塊鏈與系統間轉移資產。但要讓橋接安全是非常困難的，過去也常因漏洞而被駭。ZK 技術能讓資產轉移更快速且更安全，不需依賴可信第三方或容易出錯的方法。目前已有 zkBridge 上線，還有 Succinct Labs 等項目正在開發中 ⁴³。

隱私身份（Private identity）：隨著越來越多封閉式系統需要建立與管理我們的線上身份，我們更希望能自己掌控、整合這些分散的身份資訊，並保持其隱私。目前如 Sismo 等專案已能做到這一點，其他類似系統也正持續開發中 ⁴⁴。

以上只是一部分例子，遠非全部。我們還沒提到隱私且不可否認的聲譽系統、Web2 聲譽輸出、抗女巫攻擊的 DDoS 防護、抗脅迫的證明方式、資料複製證明、匿名空投、社交距離證明等應用 ⁴⁵。

即將出現的應用

ZK-EVM（完全等效版）：ZK-EVM 有多種版本，其中最具挑戰性的，是與以太坊完全等效的版本。其他版本可能會為了容易生成證明而做出簡化。但若能做到完全等效，就代表它與目前的以太坊系統無異，且能以一份精簡的證明驗證所有歷史區塊的正確性。你甚至可以只用一台手機，就根據數學原理驗證整條區塊鏈的完整性，無需信任他人或動用高階設備。目前由 ZK-EVM Community Edition 團隊開發中 ⁴⁶。

通用型可證明運算：世界上大部分的運算都不是在 EVM 中發生，而是在其他系統裡，例如基於 WASM 或 LLVM 的程式非常普遍 ⁴⁷。我們可以採用與 ZK-EVM 類似的方法，實作通用的私密可證明運算。例如，證明某資料庫中存在某筆紀錄，但不洩漏任何其他資料。目前已有許多團隊投入開發，如 Delphinus Labs、RISC Zero、Orochi Network 與 nil.foundation 等 ⁴⁸。

ZK 機器學習（ZK ML）：我們可以在鏈下完成某些運算，並產出一份證明來證明它確實正確執行。這表示我們可以使用私密資料來訓練更好的模型，同時不需要洩漏這些資料內容。例如，可用敏感文件、語音甚至 DNA 來找出健康風險。這種方式同時兼顧可擴展性與隱私性。目前已有 MNIST（手寫數字識別常用測試集）等概念驗證（PoC），也有人正在將神經網路引入 ZKP 中 ⁴⁹。

照片真偽驗證（Photo authenticity）：可用來驗證照片或影片的來源與真實性，包括經過標準後製編輯的情況。也就是說，我們可以證明一張照片是在某個時間、地點拍攝的，並且僅經過特定範圍內的編輯（例如縮放、裁切、轉灰階等由美聯社核可的操作）。目前已有相關研究成果與概念驗證（PoC） ⁵⁰。

合規驗證（Compliance）：可證明一筆私密交易符合特定規範，或資產不在某個黑名單上。也可以證明一間交易所具備清償能力，而不需揭露其資產細節。Espresso Labs 等系統已有相關成果，有些系統已實作簡易版的功能。

屏蔽式與意圖（Intents）：公共區塊鏈的使用者往往有某些特定目標，這些可以透過「意圖（intent）」來表達。例如某人想將一種代幣兌換成另一種，他可以公布自己的意圖，等待與對應目標相符的人配對。這些意圖理想上應該是被屏蔽（類似 Zcash 的遮蔽交易，只洩漏交易「做了什麼」而非「誰做的」），或是完全私密的。目前 Anoma 正在開發這項技術，從遮蔽式意圖配對開始。若要實作完全私密的意圖配對，可能需重大密碼學突破。

自主世界（Autonomous worlds）：是如 Dark Forest 一般的延伸應用。一個「世界」可以是實體的，也可以是概念性的，例如納尼亞世界、基督信仰、美元體系、比特幣或普通法法律體系。當世界的規則可以被任何人改變，且不影響其客觀性時，就具備「自治」特性。0xPARC 基金會目前正以遊戲與建構世界為背景進行探索 ⁵¹。

資料真實性證明（Proof of data authenticity）：從網站應用程式匯出資料，並以私密方式證明其內容的某些事實。這項技術基於 TLS 協議，意味著它可以應用在幾乎所有現代網站上。目前由 TLSNotary 團隊開發中 ⁵²。

核武裁軍（Nuclear disarmament）：讓核查人員在不需查看敏感內部構造的情況下，確認一個物體是否為核武器。目前已有結合物理模擬的研究論文問世 ⁵³。

和平談判與高風險協商（Peace talks and negotiation）：在談判中，雙方常會有某些底線或限制，但不願揭露，避免削弱自身談判籌碼。若這些限制可以透過密碼技術明確編碼，雙方就能在不揭露具體限制值的情況下，對複雜條件進行協商並達成共識。這讓彼此不互信的人也能進行合作協商。實現這一點可能需要多方計算（MPC）技術上的突破，該技術可在秘密共享的資料上進行運算 ⁵⁴。

當然，這些應用仍然不是全部。未來勢必還會出現更多全新想像與實作。如你所見，ZK 的潛力極其廣泛，我們可以做的事情實在太多了。

你可能會好奇，為什麼這麼多應用都跟區塊鏈有關？這個問題在前一章「為什麼是現在？」中有部分解答。ZK 是一項與區塊鏈正交的技術，並非一定要搭配使用，但區塊鏈往往是個合理又實用的工具，值得一用。

同樣的，目前關注這些應用的社群與問題範圍，也大多與區塊鏈社群重疊。隨著技術日漸成熟，我們可以預期 ZK 應用中的「區塊鏈」部分將漸漸淡化成純粹的實作細節，這在某些案例中其實已經發生。再往前看，甚至連「ZK」也會從主角退到幕後，變成只是在背景使用了 ZKP 的一般應用程式。

最後，當線上通訊與相關應用的加密技術剛出現時，主要是軍方與網路公司在使用與發展這些技術。郵局或傳統的實體物流公司雖然理論上也能開發這些技術，但實際上並沒有。⁵⁵

這一節就以 Barry Whitehat 的一句話作結。他是 ZK 領域知名研究者，隸屬於 Ethereum Foundation 的 PSE（Privacy and Scalability Explorations）團隊。在被問到對 ZK 未來的預測時，他這麼說：

「到 2040 年，會有人因為使用 ZKP 而獲得諾貝爾和平獎。」⁵⁶

這樣的說法狂妄又大膽嗎？絕對是。會成真嗎？或許不會。但有可能嗎？當然。這是一個值得深思的未來想像。我們的思維模式是否能接受這種可能性，與那些立刻否定它的想法，差異究竟在哪？要讓這種情況成為現實，需要哪些條件？

ZKP 是一種全新且強大的工具，而限制我們的，往往是對它應用可能性的想像力。

結語

本節將總結本文內容，並提供後續方向

本文介紹了 ZKP 是什麼、為什麼值得關注、以及它們在哪些情境下有用。我們也探討了 ZKP 的運作方式與其技術特性，最後回顧了一些當前與未來的應用場景。

希望這篇文章能幫助你更了解 ZKP 的本質，也許還能激發一些靈光一閃的時刻，或啟發你用全新角度思考這些技術。也許它甚至能幫助你，在未來繼續追隨 ZKP 的魔法。

在後續的文章中，我們將深入探討這些主題，也會從更技術的角度切入，理解 ZKP 更細緻的原理與應用範圍。

如果你對某個特定主題特別感興趣，或有想看到的內容，也歡迎透過 Twitter 或電子郵件聯絡我。優秀的留言我會放在註腳中！

致謝

感謝 Michelle Lai、Chih-Cheng Liang、Jenny Lin、Anna Lindegren 與 Eve Ko 閱讀初稿並提供寶貴建議。

感謝 Nicole、Pinhao、Anton 協助翻譯。

圖片來源

• Where's Waldo - Unknown source, Where's Waldo originally created by Martin Handford
• Silent Reading - Jorge Royan, CC BY-SA 3.0, via Wikimedia Commons
• Sherlock Holmes - Sidney Paget, Public domain, via Wikimedia Commons
• Moon landing - Neil A. Armstrong, Public domain, via Wikimedia Commons
• Pascal's Calculator - kitmasterbloke, CC-BY 2.0, via Openverse
• Moore's law - Max Roser, Hannah Ritchie, CC-BY 4.0, via Wikimedia Commons
• Sudoku puzzle - Tim Stellmach, CC0, via Wikimedia Commons
• Magic spell - National Library of Wales, CC0, via Wikimedia Commons
• Cyberpunk - bloodlessbaron, Public Domain, via Openverse

參考資料

Footnotes

1. See A Cypherpunk Manifesto for the full text. Also see Wikipedia on Cypherpunks. ↩

2. Some people have different interpretations of this specific passage, but it is still the case that humans made the transition from primarily oral storytelling to silent reading at some point not too long ago. See Wikipedia on History of silent reading for more on silent reading. ↩

3. Original quote in French: Je n'ai fait celle-ci plus longue que parce que je n'ai pas eu le loisir de la faire plus courte. See Quote Investigator on this quote. ↩

4. Kudos to Juraj Bednar for suggesting using murder mystery as a way to explain the notion of a proof. ↩

5. Succinctness has a precise mathematical definition, but we won't go into this in this article. See ZKProof Community Reference for a more precise definition. ↩

6. Transaction costs is an economic concept. See this Wikipedia article on transaction costs. ↩

7. In a checksum, we do some basic operations like adding and subtracting the initial digits, and if the final digit isn't the same we know something went wrong. Fun fact: Unlike most similar ID systems, a Social Security Number (SSN) in the US does not have a checksum. If a checksum is just one digit long it is sometimes just called a check digit. ↩

8. While more common in less developed countries, this happened recently with bank failures in the US. See Wikipedia article on effects of Collapse of Silicon Valley Bank. ↩

9. Full quote: "It is a profoundly erroneous truism, repeated by all copy-books and by eminent people when they are making speeches, that we should cultivate the habit of thinking of what we are doing. The precise opposite is the case. Civilization advances by extending the number of important operations which we can perform without thinking about them. Operations of thought are like cavalry charges in a battle — they are strictly limited in number, they require fresh horses, and must only be made at decisive moments." See Wikiquote. ↩

10. Pascal's calculator, the Pascaline, is a mechanical calculator. It was very impressive when it came out in 1642. See Pascal's calculator. ↩

11. In well-designed authentication schemes the provider doesn't see your password either, just a salted hash of it. See Wikipedia on form of stored passwords. ↩

12. SHA256 is a an often used cryptographic hash function. See SHA2. ↩

13. You can verify this yourself with a SHA256 calculator online or do it yourself at your computer with the sha256sum utility. ↩

14. Cryptography studies how to keep information safe and hide it from adversaries. It is a blend of mathematics, computer science and engineering. You can also read more about cryptographic hash functions and their purpose here. ↩

15. Technically this is called proving knowledge of the pre-image of a hash. ↩

16. See the Federalist Papers. ↩

17. See this article on group signatures by 0xPARC. Includes the relevant Circom code. ↩

18. Zero Knowledge Proofs have existed since 1985, and the authors later won a Gödel Prize for their work. We can compare this to public-key cryptography, which took many decades until it was used for things like TLS, a now indispensable building block for secure Internet usage. ↩

19. For example, Lambda calculus with Church numerals and Lisp were initially theoretical and largely unpractical when first proposed. Dan Boneh and others have made the observation that making prover time quasilinear is what really made ZKPs practical, even in theory. ↩

20. See the origins of Zcash, the Zerocoin paper. ↩

21. Censorship-resistance means anyone can transact on a public blockchain without permission as long as they follow the basic rules of the protocol. It also means it is very costly for an attacker to alter or disrupt the operation of the system. Transparency refers to transactions being publicly auditable and immutable on the blockchain forever. These notions are closely related to decentralization and security, and are a big part of the value proposition of public blockchains compared to other systems. ↩

22. BLS signatures used in the Ethereum Consensus Layer were deployed and used to secure billions of dollars just a few years after it was developed. See Wikipedia for more on BLS Signatures. ↩

23. Dan Boneh, an applied cryptography professor at Stanford, is a great example of this in terms of his involvement in various cryptocurrency-related projects. ↩

24. Thee author heard about this from gubsheep at 0xPARC, but it has popped up a few times. This also matches the author's own experience, working on RLN and noticing 1-2 order of magnitude improvements in things like prover time in a few years. ↩

25. In a legal setting, false positives do happen, see for example the Innocence Project. In a mathematical setting we can make this false positive rate very precise, and it isn't even close to a fair game. That's the power of mathematics. We'll look at this more in future articles on probabilistic proofs. ↩

26. You'd probably want to ask Sherlock Holmes some follow-up questions first though, before throwing our prospective murderer in jail. It is possible Sherlock Holmes is trying to fool you! In ZKPs we assume the prover is untrusted. ↩

27. This is done using the Fiat-Shamir heuristic. ↩

28. Sometimes people make a distinction between these two, but it is a technical one (computational vs statistical soundness) and not something we have to concern ourselves with right now. See ZKProof Community Reference for more. ↩

29. Alice and Bob are commonly used characters in cryptographic systems, see Wikipedia. ↩

30. There are also zk-STARKs, so one could argue a more accurate name might be (zk)S(T|N)ARKs. This is obviously a bit of a mouthful, so people tend to use ZK as a shorthand. See for example the name of the ZK podcast, the ZK proof standard, etc. ZK is the most magical property of ZKPs, in the author's opinion. ↩

31. Setups are multi-faceted and a big part of the security assumptions of a ZKP. They are a bit involved mathematically, and to give them full justice would need a dedicated article. There's a great layman's podcast on The Ceremony Zcash held in 2016 that you can listen to here. ↩

32. Technically speaking this is an arithmetic circuit (dealing with numbers), but we won't introduce details of this in this article. See ZKProof Community Reference for more. ↩

33. Unless you want to! ZK is sometimes called "Magic Moon Math", but if you really study it the mathematics you need to get an intuition for how they actually work under the hood isn't as complex as you might think. We won't go into it in this article, though. Here's a presentation by the author on some of the mathematical foundations of ZKPs. ↩

34. French for here you go, presto, bingo, ta-da, and Bob's your uncle. ↩

35. There are different notions of succinctness, and this depends on the specific proof system. Technically, we call proofs succinct if they are sublinear in time complexity. ↩

36. Allegedly a quote by William Gibson, see here. ↩

37. With many new versions being developed, like Aztec and Railgun. Tornado Cash (archive) works quite differently from Zcash, acting more as a mixer. Tornado Cash was also recently sanctioned by the US government. As of this writing there are still a lot of unknowns about this case, but it was a controversial event that lead to lawsuits. Some see this as a sequel to the Crypto Wars in the 1990s. There are other alternatives like Monero and Wasabi Wallet, that are not based on ZKP but have similar design goals. Read more about the Case for Electronic Cash by Coin Center. ↩

38. See Semaphore by the Privacy & Scaling Explorations team. ↩

39. This is similar to how the traditional banking system works too, where there are multiple layers of settlement happening. It is just hidden from most end users. See L2Beat for an overview of different Layer 2 solutions, including ZK Rollups. Also see Loopring, dYdX. and Starknet. ↩

40. There are different types of zkEVM, and the difference can be quite subtle. See this post by Vitalik for more on the difference. Also see Polygon zkEVM, zkSync Era. ↩

41. Mina allows for succinct verification of the whole chain, whereas Aleo focuses more on privacy. Also see Mina and Aleo. ↩

42. In Dark Forest, some people write very complex bots that play the game on its own. They even form private DAOs and create smart contracts that play the game semi-autonomously. ↩

43. Succinct Labs made Telepathy is one such project. zkBridge is another. There are likely many others. ↩

44. Proof Carrying Data by 0xPARC, is one such example. See PCD. Also see Sismo. ↩

45. We won't go into these here, but I encourage the curious reader to search the web to find out how various projects are using or thinking about using ZKPs to achieve their design goals. Example: Unirep, Interep, RLN, RLNP2P, MACI, Filecoin, Stealthdrop, ETHDos, and many more. ↩

46. See ⁴⁰ above for more on this distinction. ↩

47. LLVM and WASM are compiler and toolchain technologies. Very roughly speaking, they allow you to write code in different programming languages that run in different types of environments, such as in different web browsers and on different types of computers. Understanding the specifics of these systems isn't important for our purposes, just that they allow us to write and use programs in many different environments. See LLVM, WASM. ↩

48. See Delphinus Labs, RISC Zero, Orochi Network, nil.foundation. ↩

49. See zk-MNIST and EZKL. There are also projects doing things like neural networks in more modern efficient proof systems like Nova. ↩

50. See article on fighting disinformation with ZK. ↩

51. See this essay by ludens at 0xPARC for more details on this idea. ↩

52. See TLS Notary ↩

53. See article (archive) ↩

54. Unlike Zero Knowledge Proofs, which allow you to make statements about private data, Multi-Party Computation (MPC) generalizes this concept and allows us to do computation on shared secrets. That is, if Alice and Bob have their own secret, we can write a program that combines these two secrets in some non-trivial way, without revealing anyone's secrets. This is what we want in a negotiation setting, because we want to compare stakeholder's private information in some way to reach an acceptable compromise. Most MPCs that exist today are quite limited and inefficient, but it is an exciting area of research with a lot of potential. ↩

55. A familiar story: see Sears vs Amazon. ↩

56. Quote from a panel at Devcon5. ↩