Understanding The Math Behind ZKPs

Introduction

In this article we'll explain the math behind ZKPs. Accessible to a smart high school student, or a rusty STEM graduate. Develop intuition for how things work under the hood, and build a foundational framework for the key concepts involved. Accompanied by a toy implementation in less than 100 lines of code. No polynomials or elliptic curves necessary.

Prerequisites

We assume two things:

• You are familiar with the basics of ZKPs. High level is fine, for example by reading a friendly introduction to Zero Knowledge.
• You aren't afraid of squiggly symbols (aka math). This text assumes you are either (a) a STEM graduate ¹ who has taken a course in math a long time ago, or (b) you are a smart high school student who likes math. You don't need a formal background in computer science, mathematics, or cryptography.

The main requirement is curiosity and drive to learn. If you are lacking knowledge about a specific topic, you can easily look it up ². We deliberately keep the mathematical pre-requisites few and use basic math.

While it is useful to have read both previous articles, strictly speaking only the first is required.

In terms of math background, these are things you should ideally have a basic understanding of:

• System of equations (solving more than one equation at a time)
• Modular arithmetic (clock math)
• Boolean functions (AND, OR)
• Hash functions (like SHA256)
• Notion of randomness (random number)
• Basic probability (random coin toss)
• Prime numbers (knowing they exist)
• Basic math notation (checking equality; $a_i$ means the $i$-th subscript)

Even if you aren't fluent in the above, you'll probably pick things up by osmosis.

Overview

Here's an overview of how we will proceed. All of these concepts will be introduced in their respective sections, so don't worry if all these terms don't make sense to you right now.

We'll start by going over some key concepts. These are foundational building blocks such as: circuits, functional completeness, commitments, secret sharing, and sigma protocols.

After that we'll look at a specific ZKP protocol: ZKBoo ³. ZKBoo is a very simple protocol, and is excellent for developing intuition for how things work under the hood. It does so without requiring more advanced mathematics, such as elliptic curve cryptography.

We'll start by using secret sharing to prove a simple constraint, then build on it from there. Making the protocol interactive with a sigma protocol, functionally complete, and proving multiple constraints. We'll improve the security, the soundness, of it by performing the protocol multiple rounds. Then we'll make it non-interactive using the Fiat-Shamir transform.

You'll understand exactly how we can prove this set of constraints to a Verifier, in a way that is sound, non-interactive, and maintains zero knowledge of some variables:

After having completed our basic ZKBoo protocol, we'll see how ZKBoo connects to other zkSNARKs you might have heard about. We'll see what ZKBoo is missing, and lay the groundwork for comparing it against different modern ZKP protocols.

Finally, there are some related topics in the appendix. In Appendix A, we see how the core of ZKBoo can be implemented in just ~50 lines of code using SageMath ⁴ - remarkably compact. A toy version of the entire protocol still fits in under 100 lines. There's also a link to a Github code repo for further exploration.

Appendix B shows how to generalize our boolean circuits to arithmetic circuits. In Appendix C, we include some more mathematical definitions of zkSNARKs.

Let's get started.

Key Concepts

In the following section we introduce some key concepts, such as circuits, functional completeness, commitments, secret sharing, and sigma protocols.

Circuits

In a ZKP we are proving that we know a secret, such that applying some computation on it results in some specific output, without revealing the secret itself. The computation is made up of some set of constraints that all have to be satisfied. We can model this as a circuit.

For example, we can express a computation as satisfying the following set of constraints:

In this case, $a, b, d$ are private input, and $e$ is public output ⁵. $c$ is determined by $a, b$, and is thus an intermediate variable.

We can visualize this as the following circuit:

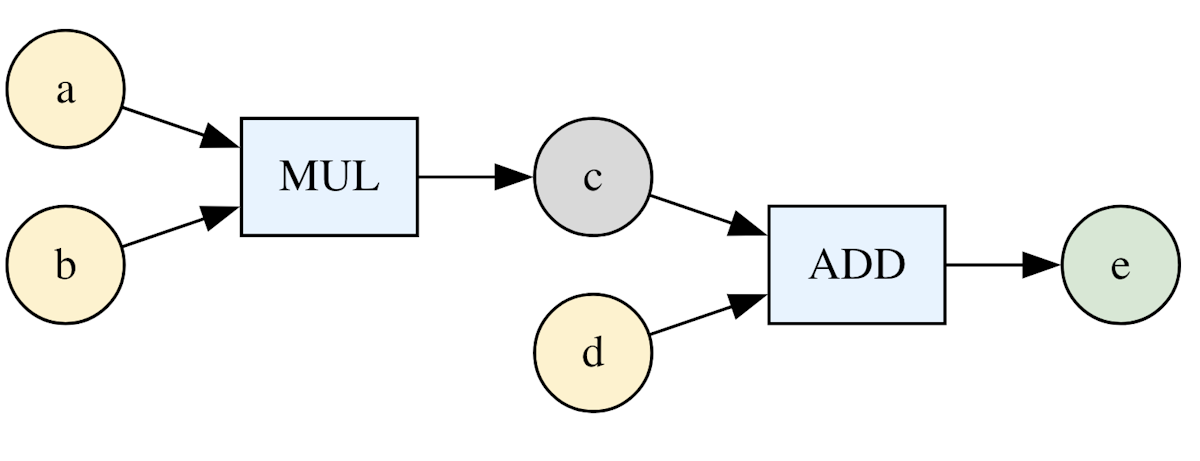
Unlike a normal computer program, constraints are unordered. It doesn't matter which order constraints are defined in, as they all have to be satisfied ⁶. This means there's no real difference between public input and public output, mathematically speaking.

We often split up the different types of variables as ⁷:

• Witness variables - private variables, known only to the Prover
• Instance variables - public variables, input or output, known both to Prover and Verifier

Different people use different words, so it is useful to be be aware of different ways of referring to these variables. Mathematically speaking, we can express the circuit above as:

Where $x$ is the public variable ($e$), $w$ the witness variables ($a, b, d$). That is, we have:

What we are doing when we are proving a ZKP is proving that a set of equations hold, without revealing information about some set of private variables or witness. ⁸

Functional Completeness

How do we connect the equations or constraints we are solving to a computer program? The simplest way to understand this is to start with the most primitive example: boolean circuits.

If all the values are boolean, $0$ or $1$, we call it a boolean circuit. In boolean algebra all values are 0 or 1. We can define simple logical gates, just like in an electronic circuit (hence the name, circuit). For example, XOR is exclusive-or and can be illustrated by the following truth table:

It turns out that we only need two logical gates, XOR and AND in order to express any computation possible. This is called functional completeness ⁹, and means we can express any truth table with only these two operations.

In the circuit mentioned in the previous section we are relying on addition and multiplication. If we operate on boolean values, it turns out that these are equivalent:

That is, XOR behaves like ADD and AND behaves like MUL. For example, $1+1 = 0$ in boolean algebra (modulo 2). Similarly, we can easily express OR and NAND (NOT-AND) gates like this:

With simple boolean gates like this we can build a modern computer. To understand how this is possible, there's a book and course called From Nand to Tetris that shows how you can build a modern computer from scratch with a simple NAND boolean gate. ¹⁰

The ZKP system we will look at is called ZKBoo, which was originally defined for boolean circuits. In the text below, we'll instead assume arithmetic circuits which operate on "normal integers" ¹¹. In Appendix B, we look at how we can "justify" arithmetic circuits mathematically speaking. For now all you need to know is that we can generalize the above, and we'll be using normal integers like $1, 4, 7$ etc as values for our variables.

Commitments

We previously introduced commitments in Programming ZKPs: From Zero To Hero ¹². We'll briefly recap them here.

Commitments allow us to commit ("promise") to some value without revealing it. We commit in such a way that we can't change our mind about what we committed to. There are many types of commitments, but the simplest is to commit to a single message, and to use a hash function like SHA256 to do so ¹³.

Commitments have two key properties:

• Binding: Once you commit you can't change your mind about what you committed to
• Hiding: The commitment doesn't leak any information about the value we committed to

They allow us to do two operations:

• Commit: Commit to a specific value while keeping it hidden
• Reveal: Reveal the value so it can be verified to be correct (matching what we previously committed to)

Reveal is also sometimes called "open" in the cryptographic literature.

When we commit to a message, we add some randomness to it. This makes it harder to brute-force the message being hashed if the message can be easily guessed. For example, if you know the message is a number from 1 to 100, you can simply try all combinations until you recreate the commitment.

Committing using a hash function might look like this:

Here we concatenate ($||$) the message $m$ with some randomness $r$. Using a hash function, like SHA256, ensures we can't easily retrieve the message from $\text{com}$.

More concretely, we might have:

SHA256('foobar213151') = '419d....1611'

This takes the message foobar, adds some randomness to it and we get a commitment, a hash 419d...1611 as a result. If we give this commitment to someone else, we can later choose to reveal value $m, r$. That person can then verify that our commitment matches our original message $m$.

Commitments are very common in cryptographic protocols because they allow us to (a) bind to values (b) hide them. Specifically they are one of the key components in ZKBoo.

Secret Sharing

Another key component of ZKBoo is secret sharing. The key idea is to split up a secret into multiple parts, so you can't reconstruct it without having all the parts.

If we have a value $x$ we can split it up as follows: $x = x_1 + x_2 + x_3$ Where $x_1, x_2, x_3$ are some randomly selected values that add up to $x$.

If we give the values $x_2$ and $x_3$ to someone this doesn't tell us anything about what $x$ or $x_1$ is. For example, if I have $7 = 4 + 2 +1$ with $x=7, x_1=4$ and I give you $2$ and $1$ there's no way for you to find out what x is. We could have $x=4, x_1 = 1$, $x = 5, x_1=2$, etc ¹⁴.

In the context of ZKBoo this type of secret sharing of variables is also called MPC-In-The-Head. MPC stands for multi-party-computation ¹⁵, and traditionally it consists of multiple actors (people, servers) all coming together to do some computation together. While MPC can get quite complex, in this case it is "in the head", so we are simply simulating it in our own head. You can imagine you have three actors inside your head and you give them a share of the secret each. You can visualize these secret shares as puzzle pieces, and you need all of them to see the full picture ¹⁶:

Sigma Protocol

By combining commitments and secret sharing into a so-called sigma protocol we have all the ingredients we need for ZKBoo. A sigma protocol is a protocol that consists of two parties, a Prover and a Verifier. They exchange three messages as follows: commitment, challenge and response.

Because it consists of interactions between two parties, it is also an interactive protocol. It is called a sigma protocol because the interaction resembles the Greek letter Sigma, $\Sigma$ ¹⁷. A sigma protocol allows a Prover to, in an interactive fashion, convince a Verifier that some statement is true, without revealing some secret information. You can think of it as a primitive ZKP.

By committing to some values first, the Prover can't change their mind about those values. After that, the Verifier challenges the Prover with some tricky question. The Prover responds, and if the Verifier is happy with the response they are convinced.

Many different sigma protocols exists ¹⁸. Generally they all have the following key properties ¹⁹:

• Completeness: If a Prover knows the solution to a set of constraints, they can always convince the Verifier
• Soundness: The Verifier is only convinced if the Prover actually knows the secret; if the Prover tries to cheat, then the probability to succeed is negligible
• Zero-Knowledge: The Verifier doesn't learn anything about the Prover's secret, except that they have a valid solution

The above might seem a bit abstract, but it will become a lot more concrete once we see how this is used in practice for ZKBoo.

What follows are some simple exercises to check your understanding.

Exercises

1. In $x + 1 = y; y + 5 = z$, if $x$ is something the Prover wants to keep secret, what is the witness variable and public output?
2. Why does the order of constraints not matter? What happens if we swap the order of the two constraints above?
3. Alice commits to a number using SHA256(x || r). If she later claims she committed to 42, how can she prove it?
4. If Bob splits x=12 into 3 shares such that $x_1 + x_2 + x_3 = x$, what is a possible set of values for $(x_1, x_2, x_3)$? Why does revealing $x_2$ and $x_3$ not give us any information about $x$?
5. In a sigma protocol, why does the Prover have to commit before the Verifier sends the challenge?

ZKBoo

In this section we explain how ZKBoo works. We gradually build up from one addition constraint, to multiple constraints, to a complete interactive protocol. Then we make it statistically sound and finally we make it non-interactive.

ZKBoo is a simple ZKP protocol. It is based on boolean circuits, commitments, secret sharing (MPC-in-the-Head) and sigma protocols. It is currently not used a lot in practice, primarily because people prefer proof systems with smaller proofs ²⁰. So why learn it?

It is conceptually very simple. This means you can understand all the math behind it and implement it yourself. It doesn't require advanced mathematics or a lot of cryptography to grok. This makes it ideal for building intuition for how the math behind ZKPs work in practice. Once you understand a ZKP protocol in detail, it is a lot easier to compare it with other ZKP protocols. We'll look at this towards the end of the article and in future articles. This will help you make informed decisions about what ZKP protocol to use under what circumstances.

Splitting our variables with secret sharing

Recall the system of equations from earlier:

To simplify, let's focus on proving $c + d = e$, where $c,d$ are private and $e$ is public. Using secret sharing, we split each variable into three random shares:

The shares must preserve the relationship $c + d = e$, meaning $c_i + d_i = e_i$ for each $i$. In the MPC-in-the-Head paradigm each column with subscript $_1, _2, _3$ corresponds to an "actor" in your head, holding part of the secret. We can visualize the secret shares in the following table format:

Here's how we split these variables to achieve this:

• For the first row, we randomly generate $c_1, c_2, c_3$ such that $c_1 + c_2 + c_3 =c$
• For the second row, we do the same thing for $d_1, d_2, d_3$ and $d$
• For the third row, we set $e_1 = c_1 + d_1$, $e_2 = c_2 + d_2$, and $e_3 = c_3 + d_3$, ensuring that $e = e_1 + e_2 + e_3$

If the Verifier challenges the Prover to reveal two random columns, e.g. $(2,3)$, they check that:

Because the shares are generated randomly, revealing two columns doesn't provide any information about $c, d$, while still proving the relationship holds.

Going forward, we won't make the table with rows or columns explicitly, but you can always draw it out for yourself. Just remember that a column corresponds to a share.

Sigma protocol for ZKBoo

As a Prover, you want to convince the Verifier that you know $c$ and $d$ that fulfill the equation above, without revealing them. Here's how we'll achieve this, with a sigma protocol.

6. Prover commits to each column, $1..3$ and sends this to the Verifier
7. Verifier challenges the Prover by asking it to reveal two columns, $(i, j)$
8. The Prover responds with the values from the columns that the Verifier asks for

Once the Verifier has those values, it'll perform two checks:

• Consistency check: verify that the values add up, e.g. $c_i + d_i = e_i$
• Commitment check: verify that the commitments matches the values Prover responded with

If both of those checks pass, then the Verifier is reasonably convinced ²¹ that the Prover knows $c$ and $d$. When committing, the Prover also uses some randomness to make sure the values can't be brute-forced. By using the hiding properties of commitments and secret sharing, the Prover doesn't reveal anything about $c$ and $d$ itself.

Here's a diagram of this sigma protocol:

This achieves the three properties we care about:

• Completeness - The Prover knows a solution, and they can always convince the Verifier
• Soundness - The Verifier is only convinced if the Prover actually knows the secret (we will look at the case where the Prover is cheating next)
• Zero-knowledge - The Verifier doesn't learn anything about $c$ and $d$ (except that they add up to $e$)

While committing to values per column means the Prover can't later change their mind about the content of those columns, there are still some problems. What if the Prover guesses which columns the Verifier will challenge them with? There are only three possible options $(1,2), (1,3), (2,3)$. If so, they can cheat by only making sure those columns add up, without knowing $c$ and $d$. This means there's a whopping $\frac{1}{3}$ chance of cheating!

This touches on the statistical nature of soundness. In cryptography in practice, probabilities often play a role in ensuring security. The goal is to reduce the risk of cheating to a negligible -astronomically so - level. We'll see how to do that soon, using multiple rounds of the protocol.

But first, let's see how we deal with multiplication and multiple constraints.

Supporting multiplication

Let's go back to our original set of constraints:

Addition like $c+d=e$ was easy enough. What about multiplication? We want to decompose the relationship $a \cdot b = c$ into secret shares. How can we do this?

First we notice the following. If we naively split $a, b, c$ and set $c_i = a_i \cdot b_i$, this doesn't work. Why?

This is because multiplication is not linear, so we get cross-terms:

We need to find a better way of assigning $c_i$ to keep the relationships consistent. We can do this by splitting the cross-terms evenly across each share ²²:

Now the relationship holds. We have:

However, there's a new problem. As we reveal two columns, say $(1,2)$ we leak information about the third one. With $(1,2)$ we reveal some information about the third column through the factors $a_2 b_3 +a_3 b_2$. Depending on what the values represent, the Verifier might be able to infer what $a_3$ and $b_3$ are.

We can get around this by adding some randomness:

Now, we still have $c = c_1 + c_2 + c_3$, because all the random variables cancel out:

By adding some randomness, we don't reveal any information about the third column. We are thus using randomness to mask sensitive information, a common trick used in cryptography.

Where does $r_1, r_2, r_3$ "belong"? We add them as another variable. Seen as a table with rows and columns, we have:

where $c_1$, $c_2$, and $c_3$ are set as above. Notice how revealing columns $(1,2)$ reveals $r_1$ and $r_2$ but leaves $r_3$ unknown, thus masking the third column's value.

Putting it all together

Finally, to combine the above with the original set of constraints:

As a Prover, we:

• Set $a, b, d$ shares randomly, as above
• Set $c$ such that $a \cdot b = c$, and same for all shares
• Set $e$ such that $c+d=e$, and similarly for all its shares

Here's our updated sigma protocol with commitment-challenge-response:

Verifier does (a) consistency checks and (b) commitment checks.

Consistency check for each constraint:

• Verify $a \cdot b = c$ for shares:
  • $c_i \stackrel{?}{=} (a_i b_i + a_i b_j + a_j b_i) + (r_i - r_j)$,
  • $c_j \stackrel{?}{=} (a_j b_j + a_j b_k + a_k b_j) + (r_j - r_k)$
  • Note that $r$ subscripts $i, j, k$ are $\mod 3$
• Verify $c + d = e$ for shares: $c_i + d_i \stackrel{?}{=} e_i, \quad c_j + d_j \stackrel{?}{=} e_j$

Commitment checks:

• $com_i \stackrel{?}{=} \text{hash}(a_i, b_i, c_i, d_i, e_i, r_i), \quad com_j \stackrel{?}{=} \text{hash}(a_j, b_j, c_j, d_j, e_j, r_j)$

In the above, $r_k$ corresponds to the $k$-th column, which is not revealed. Depending on how we perform multiple rounds, this may or may no be revealed. We still check $c_i$ though, since the $i$ and $j$-th columns are revealed.

With this, we have proven a set of constraints using addition and multiplication, thus demonstrating functional completeness. We did so in a way that kept the private values private, and convinced the Verifier that the Prover knows them. Next, we'll look at how to improve the soundness by running the protocol multiple rounds.

Improving soundness

Let's look more critically at the sigma protocol we specified above. What if the Prover cheats? Let's say she guesses that the Verifier will pick column $(2,3)$. Then she doesn't actually have to know the private values. For example, in $c +d =e$ they don't have to know $c$ or $d$, $c_1$ or $d_1$. She can just make up values that make the consistency check succeed. This is because the verifier only checks the second and third column.

Recall the checks the Verifier performs:

• Consistency check: $c_i + d_i \stackrel{?}{=} e_i, \, c_j + d_j \stackrel{?}{=} e_j$
• Commitment check: $com_i \stackrel{?}{=} \text{hash}(c_i, d_i, e_i, r_i), \, com_j \stackrel{?}{=} \text{hash}(c_j, d_j, e_j, r_j)$

More concretely, we can just pick random values for $c_2, d_2$ such that $c_2 + d_2 = e_2$, and likewise for $c_3, d_3$. This doesn't require any knowledge of $c$ or $d$. Assuming the Prover thinks $(2,3)$ will be picked, then the Verifier is only checking that $c_2 + d_2 = e_2$ and $c_3 + d_3 = e_3$. This is no good.

Of course, due to the commitments, the Prover can't change their mind. if we didn't have this commitment check then they could cheat every single time. That's why we need the binding property of commitments, and why the commitment is communicated before the Verifier decides which shares to look at.

What is the probability of guessing correctly? There are three choices of two columns: $(1,2), (1,3), (2,3)$. This means there's a $\frac{1}{3}$ chance of cheating ²³. We call this the soundness error. We'd like to reduce this to a much smaller probability.

How can we do this? Turns out we can do this by doing the sigma protocol multiple rounds. Each time the Verifier picks a new set of two random shares. Of course, after the Verifier has picked, say, $(1,2)$ and $(2,3)$ they know the values of all three shares and can easily reconstruct the original $c$ and $d$, which is no good.

The way we get around this problem, but still keep the probability of cheating low, is to create new secret shares every round. For a given variable, we split it as $x = x_1 + x_2 + x_3$, where $x_1, x_2, x_3$ are random values to make the equation hold. We do this for every variable. The Verifier performs the challenge, asking for two shares, and performs consistency and commitment checks. In the next round, we again use new random shares to split our variables. This way, the Verifier can't combine the information they received in different rounds, because all they are seeing are different random shares.

With this, what is the probability of cheating? For the addition constraint above, each run it is $\frac{1}{3}$, and if we do $n$ runs we get:

If $n$ is sufficiently large, the probability of cheating is negligible. For example, if we do 100 rounds we get a probability of $(\frac{1}{3})^{100} \approx 10^{-48}$. This is extremely low. For additional security, we can just run more rounds. For more details on soundness error, see footnote ²⁴.

While this is a lot more secure, this requires a lot of interactions between the Prover and Verifier. For each round we need to send 3 messages, and for 100 rounds that's 300 messages back and forth! That's not very practical in the real world. To address that, let's look at how can make this protocol non-interactive, and get that down to a single message with the use of the Fiat Shamir Transform.

Fiat-Shamir Transform

We managed to make the protocol statistically secure by running multiple rounds. Here's the sigma protocol we had for a single round:

The goal of the Fiat-Shamir Transform is to turn this interactive protocol into a non-interactive one, where the Prover sends a single message, a proof, and the Verifier has all the information they need to verify the proof.

Why is the Verifier sending the challenge after the commitments in the first place? Because he doesn't want the Prover to change her mind and cheat by choosing the columns on their own. This would break soundness. From the Prover's point of view, this selection is random. Can we get this randomness somewhere else? Without having the Verifier generate it?

Enter the Fiat Shamir Transform. The key idea is to replace the randomness the Verifier is using with a deterministic hash function. Because hash functions are pseudo-random ²⁵, we can use this to generate a random number, that is then used to randomly select two columns.

At a high level, instead of this:

We do this:

The challenge should be produced with a hash, and include commitments as well as some public information. It is something the Prover and Verifier silently agree on, not something the Prover can decide on their own. In fact, we don't even need to send the challenge, since it can be calculated by both parties. The Prover creates commitments, computes the challenges and responses - all locally - and sends this to the Verifier. The Verifier then notes the commitments, recomputes the challenge on their own, and verifies responses and commitments.

How is the challenge computed? Why does this work? As input to our hash, we use some public information, and this acts as a "random seed" ²⁶ that neither the Prover or public controls the output for. This means we don't have to communicate this information, but can just compute this source of randomness on their own. Here's what the challenge might look like in practice:

By adding some public information <public info>, such as name of the circuit (e.g. zkboo-example) and public input (e.g. e's value 5) the Prover herself doesn't control all the input to the hash function. It is also crucial that we include all commitments as input to this hash function, so the Prover can't change her mind about what they committed to. Since hash functions like SHA256 are deterministic, the Verifier will re-create the same challenge, assuming they have access to all its input.

In our case, the Verifier is choosing two columns $(i,j)$ out of 3. There are three possibilities, so we can simply take our random hash and perform $\mod 3$ on it to get a column selection deterministically.

If we only do one round, it is quite easy for the Prover to just cheat by guessing what columns will be chosen, create commitments and compute the challenge. If the challenge results in them "guessing correctly", then they can create a fake proof. If they don't, they can tweak the inputs to create slightly different commitments, and hope they get lucky next hash run. After all, this is all done locally, so the Verifier is not aware of this.

This is why it is crucial we run multiple rounds of the protocol. And specifically, we need to use each previous round as input to the next rounds challenge. Only then can we achieve the same soundness guarantees ²⁷.

To ensure soundness, the challenge for each round must depend on all previous commitments. This prevents the Prover from "backtracking" to generate favorable outcomes. We compute the challenge for round $k$ as follows:

Where $com_{k,i}$ is the commitment for the $k-th$ round of share $i$, and <public info> is a placeholder for some predetermined shared public knowledge. By adding $k$ we ensure each round has a unique challenge, even if commitments and public info is repeated. Public info acts as a fixed source of randomness, which means neither Prover nor Verifier controls the hash output. Finally we take $\mod 3$ to make it correspond with a column choice $(i, j)$.

The Prover sends commitments and responses for all rounds. All of this information makes up the proof $\Pi$. The Verifier recomputes the challenges for each round, verifies the responses and commitments, and either accepts or rejects the proof.

Why does this work? We are using the binding property of commitments to ensure that the Prover can't change earlier inputs once challenge is generated. All challenges depends on previous commitments, and because we run the protocol $k$ rounds we guarantee soundness with very high probability.

This is great, and we now just need a single message to convince a Verifier. There's still a problem though, in that this requires quite a lot of data. Notice how each proof requires $3 \cdot k$ commitments, as well as $n \cdot k$ responses, where n is the number of variables and $k$ is the number of rounds. If we have a significant number of variables, and if $k$ is roughly 100, that results in quite a big proof.

Unfortunately, with our current tools we won't be able to make this proof more succinct. For that, we'll need to add some more tools to our toolbox. But that's for another time. We'll touch on this towards the end of the article.

If you are interested in how we jump from boolean circuits to arithmetic circuits, see Appendix B. Next let's see at how ZKBoo fits into the wider ZKP landscape.

Exercises

1. In a sigma protocol with 3 shares, where two shares are revealed, what is the probability of a cheating Prover to convince a Verifier in a single round? How does running multiple rounds help?
2. If the Prover knew in advance which columns a Verifier would choose, how could they cheat?
3. In Fiat-Shamir, why does hashing all commitments before generating the challenge make it harder to cheat?

zkSNARKs

Explains the connection with the above ZKP to zkSNARKs (Zero-Knowledge Succinct Non-Interactive ARguments of Knowledge). We break down each property and see how it relates to ZKBoo.

You might've noticed we called ZKBoo a ZKP (Zero Knowledge Proof) and not a zkSNARK, which is a term you might have heard before. While not everyone is using terms correctly ²⁸, it is useful to understand what each of these properties refer to.

Colloquially, we call ZKPs "proofs". Technically speaking, they are ARguments of Knowledge. The distinction has to do with the nature of soundness. We saw previously how we got completeness, soundness and zero-knowledge with sigma protocols. Together, the completeness and soundness properties give us "ARguments of Knowledge". In practice, we rely on computational soundness, which technically makes it an argument of knowledge and not a proof. ²⁹

The Zero-Knowledge property we have gone over; we don't reveal anything about our witness to the Verifier. Curiously, a lot of "ZK" projects and "zkSNARKs" don't actually provide the "zero knowledge" property in practice. A more accurate term to use then would probably be verifiable computation and (S)NARKs, but that sounds less sexy.

The non-interactive property (the "N" in zkSNARks) we went over. It turns out we can take basically any ZKP and make it non-interactive using the Fiat-Shamir transform. It is common to start by defining an interactive sigma protocol, and then later on make it non-interactive using Fiat-Shamir.

Finally, the property that we haven't talked about so far is succinctness. This means two things: (a) the proof is short, and (b) the proof is fast to verify. Unfortunately, this is a property that ZKBoo is missing. To get that property, we are going to need some more advanced mathematical tools. In particular, we will need polynomials and elliptic curve cryptography. We'll look into this more in a future article.

For more (still informal) mathematical details see Appendix C.

Let's look a little bit more at succinctness and ZKBoo to better understand what is going on.

On succinctness

Why is ZKBoo not succinct? When we talk about succinctness we refer to two separate properties:

• Succinct proof size: the proof is short
• Succinct verification time: the proof is fast to verify

Usually these properties are found together, but we analyze them separately ³⁰.

Let's focus on how big the proof is first. We previously noted that each proof requires some commitments and responses proportional to $n$, where n is the number of constraints, or the size of the circuit, $|C|$. When we say a proof is short, we care primarily about how the size changes as a function of the number of constraints. By size we mean how many pieces of data have to be sent, which in practice correlates with the total bytes needed to represent a proof.

We often use Big-Oh (also written Big-O) notation to describe how well a function performs as the number of elements it operates on increases ³¹. In ZKBoo's case, the proof size grows linearly with the number of constraints, or $O(n)$ in Big-Oh notation. For example, if the circuit has $n = 1000$ constraints, the proof needs on the order of 1000 commitments and responses.

With Big-Oh notation, we can talk about order of approximation without getting bogged down in details ³². Here's an illustration of some common classes of complexity:

For a proof to be succinct it needs to ideally be "sublinear". What does sublinear mean? Anything that is strictly "below" $O(n)$ in the chart above . For example, $O(\log n)$ (logarithmic) or $O(1)$ (constant) ³¹, ³³.

Intuitively, this means that as we add more constraints the size of the proof increases by less and less. The best performance is $O(1)$, where the proof size stays the same no matter the number of constraints.

What about time required to verify the proof? The Verifier has to perform consistency checks for all constraints. This is essentially equivalent to re-evaluating the whole circuit. This means verification time is linear, or O$(n)$ where n is the number of constraints $|C|$ . Thus, ZKBoo doesn't have sublinear verification time. Time here corresponds to the number of operations that a Verifier has to perform, and in practice correlates with actual "clock time". Hence, ZKBoo does not have succinct verification time.

We often want succinctness, since it means we can prove arbitrary computation in a small space (and quickly). Why doesn't ZKBoo give us this and what can be done about this?

Fundamentally, the problem is that the tools we are using are too primitive. With our current commitment scheme and secret sharing, we have to represent and evaluate all the constraints. Instead, what we can do is to use polynomials to compress our constraints into a smaller space. This leads to the idea of polynomial commitment schemes. But that's a story for another time.

Next

Hints at what is next, with polynomials, succinctness, PCS, IOP, comparison; either for a big coffee break or next article.

We've seen how to make a non-interactive ZKP end-to-end with ZKBoo. This gives us an excellent foundation for understanding the wider zkSNARKs landscape.

Here are some things to look forward to next:

• Understanding importance of polynomials, how they enable succinctness
• Generalizing commitments to polynomial commitment schemes (PCS)
• Generalizing sigma protocol to polynomial interactive oracle proof (IOP)
• Understanding PCS + Poly-IOPs framework for modern ZKP systems
• Different PCS: KZG/FRI/IPA
• Understanding different domains: server-side vs client side proving
• Grok dimensions: field size, post-quantum, setups, security assumptions
• How public blockchains can be used to verify proofs
• Why STARKs are SNARKs
• Structured vs unstructured circuits
• Other novel ZKPs

We won't go as deep on those topics, but we'll give you enough resources to feel confident to (a) either learn more or to (b) choose a zkSNARK for your specific demands.

Exercises

4. What properties do we get from ZKBoo?
5. Why is ZKBoo not succinct? Intuitively speaking.

Problems

These are optional problems that will take a bit more effort.

6. Implement multiple rounds in SageMath (see Appendix A)
7. Implement Fiat-Shamir in SageMath (see Appendix A)
8. Find a few proof systems you've heard about. Identify how they are similar and different from each other. Compare and contrast with ZKBoo.

Conclusion

Re-cap of what we went over.

In this article we started from a basic understanding of ZKPs and a minimal math background. We then introduced key concepts such as circuits, functional completeness, commitments, secret sharing and sigma protocols.

We then took those key concepts and looked at how to use them to make a ZKBoo ZKP. We looked at a set of constraints and saw how we could prove them, starting from a simple addition constraint. We saw how to make it work for multiple constraints, and how we leverage randomness in multiplication constraints. We analyzed the security of the protocol and improved its soundness by running it multiple times. Then we made the whole thing non-interactive using Fiat-Shamir.

After that, we dove a bit deeper into some specific topics. We saw how to generalize boolean circuits to arithmetic circuits using finite fields, and we went over the properties of zkSNARKs and how they apply to ZKBoo. We developed an intuition for why ZKBoo doesn't achieve succinctness. And finally, we hinted at some more advanced topics that we can explore next.

If you want to deepen your understanding, a good idea is to look at the code snippets (Appendix A) and see how you can extend or modify it. If something was confusing, feel free to reach out! Good luck on your ZK journey and see you soon.

Acknowledgements

Thanks to Hanno Cornelius, dmpierre, Aayush Gupta, Adrian Li, Chih-Cheng Liang, and r4bbit for reading drafts and providing feedback on this.

Images

• Big O cheatsheet - Eric Rowell, Public Domain, via Wikimedia Commons

Appendix A: ZKBoo Code

What follows is a code examples of implementing ZKBoo concisely in SageMath.

There's a code repo available here: https://github.com/oskarth/zkintro-math

It shows an implementation of various constructs specified in the article above. While not required, it can be useful to map the math equations to actual code. It is implemented in SageMath, which is a piece of math software on top of Python. It reads basically as pseudo-code, and it allows us to concisely express math as code.

In the repo we have the following examples:

• commitments_shares.sage - basic commitments and secret sharing
• zkboo_add.sage - basic addition constraint in ZKBoo
• zkboo_mul.sage - basic addition and multiplication constraint in ZKBoo

Extending the above to support multiple rounds and Fiat-Shamir transform is currently left as an exercise for the reader.

In total, the ZKBoo protocol can comfortably be expressed in under 100 lines of code ³⁴. Once a mathematical prototype in Sage exists, it is much easier to then "port" this to something like Python, JavaScript, Rust, or Go for real-world usage.

The following code snippet (zkboo_mul.sage) shows functional completeness for one round of interactive ZKBoo in 60 lines of code with comments. It can be extended to use multiple rounds and made non-interactive with Fiat-Shamir in less than 100 lines of code.

import random, hashlib
from sage.all import GF

p = 101
F = GF(p)

def secret_share(value):
    """Split 'value' into 3 random shares mod p."""
    s1, s2 = F.random_element(), F.random_element()
    return [s1, s2, (value - s1 - s2) % p]

def commit(vals):
    """Hash tuple of values to produce a commitment."""
    return hashlib.sha256(",".join(map(str, vals)).encode()).hexdigest()

def multiply_shares(a_sh, b_sh):
    """Compute c_i for a single gate a*b=c with offsets r_i."""
    r = [F.random_element() for _ in range(3)]
    c = [(a_sh[i] * b_sh[i] + a_sh[i] * b_sh[(i + 1) % 3] + a_sh[(i + 1) % 3] * b_sh[i] + r[i] - r[(i + 1) % 3]) % p for i in range(3)]
    assert sum(c) % p == (sum(a_sh) * sum(b_sh)) % p
    return c, r

def zkboo_Prover(a, b, d):
    """Generate shares for a,b,d and compute c=a*b, e=c+d with random offsets."""
    a_sh, b_sh, d_sh = secret_share(a), secret_share(b), secret_share(d)
    c_sh, r_sh = multiply_shares(a_sh, b_sh)
    e_sh = [(c_sh[i] + d_sh[i]) % p for i in range(3)]
    commits = [commit((a_sh[i], b_sh[i], c_sh[i], d_sh[i], e_sh[i], r_sh[i])) for i in range(3)]
    return a_sh, b_sh, c_sh, d_sh, e_sh, commits, r_sh

def zkboo_Verifier_challenge():
    """Pick two random shares to reveal."""
    return random.sample(range(3), 2)

def zkboo_Prover_response(ch, a_sh, b_sh, c_sh, d_sh, e_sh, r_sh):
    """Reveal the requested two shares with all data."""
    return [{"a": a_sh[i], "b": b_sh[i], "c": c_sh[i], "d": d_sh[i], "e": e_sh[i], "r": r_sh[i]} for i in ch]

def zkboo_verify(ch, resp, commits):
    """Check commitments and verify correctness of revealed shares."""
    if any(commit((resp[i]["a"], resp[i]["b"], resp[i]["c"], resp[i]["d"], resp[i]["e"], resp[i]["r"])) != commits[ch[i]] for i in range(2)):
        return False
    def check_c(sh_i, sh_j):
        return (sh_i["a"] * sh_i["b"] + sh_i["a"] * sh_j["b"] + sh_j["a"] * sh_i["b"] + (sh_i["r"] - sh_j["r"])) % p == sh_i["c"]
    # Ensure correct pairs of shares are used when verifying multiplication consistency
    if (ch[0] + 1) % 3 == ch[1] and not check_c(resp[0], resp[1]): return False
    if (ch[1] + 1) % 3 == ch[0] and not check_c(resp[1], resp[0]): return False
    return all((share["c"] + share["d"]) % p == share["e"] for share in resp)

def test_zkboo_single_round():
    """Test a single-round reveal for a,b,d = 3,4,5."""
    a, b, d = F(3), F(4), F(5)
    a_sh, b_sh, c_sh, d_sh, e_sh, commits, r_sh = zkboo_Prover(a, b, d)
    ch = zkboo_Verifier_challenge()
    resp = zkboo_Prover_response(ch, a_sh, b_sh, c_sh, d_sh, e_sh, r_sh)
    assert zkboo_verify(ch, resp, commits), "ZKBoo single-round failed"
    print("Single-round test passed!")

test_zkboo_single_round()

Appendix B: Arithmetic Circuits

This section explains how to generalize the boolean circuits above to arithmetic circuits.

In mathematics, there's a field called abstract algebra. It deals with different algebraic structures and operations on top of them. For example, we have things like the set of natural numbers or the set of integers:

We combine these sets with some operations, such as addition or multiplication, that work in a particular way. With this we can talk about structures like sets, groups, rings, and fields. The particular definitions of these structures aren't that important right now. The key idea is that each structure adds more capabilities:

Fields in particular allow for division (except by zero). This is because there exists a multiplicative inverse for every element in a field. Notably, this is not true for the set of integers with addition and multiplication, written $(\mathbb{Z}, +, \cdot)$ ³⁵.

For example, the multiplicative inverse of $3$ is $\frac{1}{3}$ (since $3 \cdot \frac{1}{3} = 1$), which doesn't exist in $\mathbb{Z}$, because it isn't an integer ³⁶. If we were to talk about the set of real numbers, $\mathbb{R}$ it would be fine because $0.33...$ is in it, so $(\mathbb{R}, +, \cdot)$ is a field.

Computers however work on hardware and we operate on finite numbers. So when it comes to to cryptography, we are are interested in finite fields. That is, a field with a finite set of members. For example:

A lot of cryptographic protocols require division and well-defined modular arithmetic. It turns out that we can construct a finite field by simply restricting it $\mod p$, where $p$ is a prime number ³⁷. We write this either as $\mathbb{F}_p$ or $\mathbb{GF}(p)$. The $\mathbb{GF}$ stands for Galois Field, which is another name for finite fields ³⁸.

In the example above, if we exclude $0$ (since division by $0$ is not allowed; indicated by $^*$), we have:

We can see that each element has a multiplicative inverse in the set. For example, $2 \cdot 3 \mod 5 \equiv 1$.

In ZKBoo above, we are using $\mathbb{GF}(2)$, the simplest finite field, for boolean circuits. Arithmetic circuits generalize this to $\mathbb{GF}(p)$, where $p$ is a prime number. This means all operations, addition and multiplication, are performed $\mod p$, ensuring values stay within that field. This allows us to work with numbers larger than 0 and 1. In this field, addition and multiplication work well, so we can perform well-defined modular arithmetic. We can use integers as we expect to, as long as they are bounded by (less than) a specific prime number. In practice, we often use very large prime numbers ³⁹. This means we can express very large numbers and arithmetic around it in a well-defined manner.

Appendix C: zkSNARKs math definitions

Let's make the section on zkSNARKs above a little bit precise, while still keeping it mathematically informal ⁴⁰. Feel free to skip this appendix if you are satisfied by the main text.

Completeness - for all $x, w$ in $C(x,w)$ the probability that the Verifier V accepts Prover's proof $P(x,w)$ is 1. That is:

Soundness - V accepts proof $\pi$ $\implies$ P "knows" $w$ s.t. $C(x,w) = 0$, and if proof $\pi$ is false, $Pr[\text{V accepts } \pi] \leq \text{negligble probability, e.g }2^{-80}$ ⁴¹

Zero-Knowledge - $C(x, \pi$) with proof $\pi$ reveals nothing about $w$

Succinctness - proof $\pi$ is "short" and and $V(x, \pi)$ is "fast" to verify.

Short has different definitions, but usually it means $\text{len}(\pi) = \text{sublinear}(|w|)$, where $|w|$ is the size of the witness ³³.

Fast to verify means $\text{time}(V) = O_{\lambda}((|x|, \text{sublinear}(|C|))$, where $O_{\lambda}$ means "order of" in Big-Oh notation ³¹, and $|C|$ is the size of the circuit.

Sometimes quasi-linear, e.g. $O(n \log n)$, is accepted as being "succinct enough".

Non-interactive - It is enough for Prover to send $\pi$ to Verifier to convince them, the Verifier can verify proof with $x$ and $\pi$. ⁴²

References